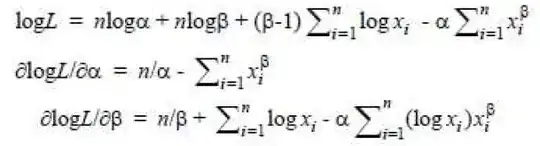Here's why you can (hopefully) use $R^2$ for non-linear models. Why not?

Question

We calculate $R^2$ as follows:

$R^2 = 1 - \frac{\|y - \hat y\|^2}{\|y - \bar y\|^2}$

1. $y$ is a vector of true answers;
2. $\bar y$ is a vector whose elements are mean of $y$;
3. $\hat y$ is a a vector with our model's predictions.

So, in case of OLS Linear Regression $R^2 = 1 - \sin^2 \theta = \cos^2 \theta$, where $\theta$ is an angle between vectors $y - \bar y$ and $\hat y - \bar y$.

Everybody says that it's forbidden to use $R^2$ in case of non-linear models. So, I've been pondering and trying to imagine why it is so and still disagree with that. Here is my line of reasoning. Suppose we have some non-linear model and here is all you need to know about it:

You can see from this GIF that $\hat y - \bar y$ is not orthogonal to $y - \hat y$. So, $SS_{tot} ≠ SS_{exp} + SS_{res}$, where $SS_{tot} = \|y - \bar y\|^2$, $SS_{exp} = \|\hat y - \bar y\|^2$ and $SS_{res} = \|y - \hat y\|^2$. It's obvious from the Pythagorean theorem. But why do we need that equality to be true? Look at how we calculate $R^2$. We don't actually calculate $SS_{exp}$ explicitly. Instead we calculate it as a difference between $SS_{tot}$ and $SS_{res}$.

Let's look at what's happening when we calculate $R^2$ in the case of our non-linear model:

When you calculate $\|y - \bar y\|^2 - \|y - \hat y\|^2$ in the numerator according to the Pythagorean theorem it is equivalent to calculating the squared length of the vector $(\hat y) - \bar y$. It just means that if your model was linear, then your best fit solution would lie where the green point $(\hat y)$ is lying. $R^2$ is $\cos^2 \theta$. But now $\theta$ is no longer the angle between vectors $y - \bar y$ and $\hat y - \bar y$, but between vectors $y - \bar y$ and $(\hat y) - \bar y$.

There are actually infinitely many points $\hat y$ such that $\|y - \bar y\|^2 - \|y - \hat y\|^2$ is equal to $\|(\hat y) - \bar y\|^2$. For every red point that's true:

From here we can't say that $\left((\hat y) - \bar y\right) + \left(y - \hat y\right) = \left(y - \bar y\right)$, but the variance of $y$ decreased exactly by $\|(\hat y) - \bar y\|^2$, because $\|y - \bar y\|^2 - \|(\hat y) - \bar y\|^2 = \|y - (\hat y)\| = \|y - \hat y\|^2$. And the closer the red point $\hat y$ is to $y$, the smaller is the value of $R^2 = \cos^2 \theta$.

This is as much meaningful as it is in case of OLS Linear Regression. So, if everything I said was right, then why can't we use $\mathbf{R^2}$ for non-linear models? If $R^2 = 0.86$ then your model's variance decreased by $86\text%$ (no matter linear or not).

Answer 1

We can use $R^2$ for nonlinear models. In a model comparison, higher $R^2$ means lower $MSE$, even if the models are nonlinear. However, because of the lack of orthogonality, $R^2$ loses its interpretation of proportion of variance explained, so its use as an absolute measure of model performance (“Sure, model A beats model B, but is model A any good?”) is limited.

(For $MSE$, I assume that we divide by $n$ or $n-1$, not $n-p$.)