Linear regression has two assumptions about the residuals :
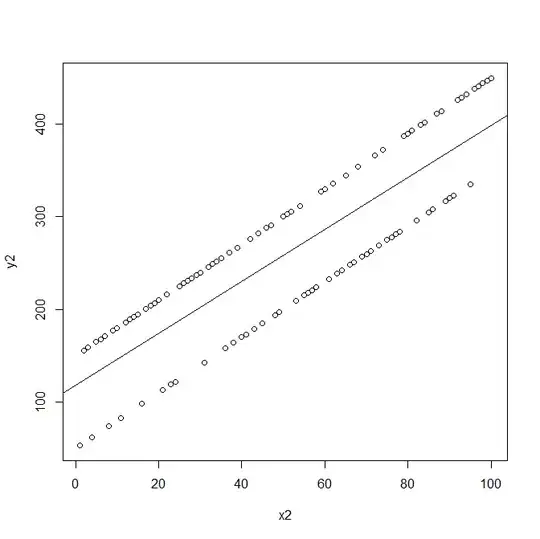
The residuals should have constant variance (for every level of the predictor).
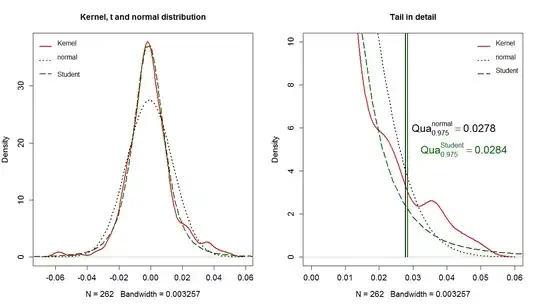
The residuals should follow a normal distribution.
Is it possible to visualize how would the data itself, not the residuals, look like if one of these assumptions is violated?
I am seeking a visual example that would demonstrate clearly why these assumptions are necessary.