When you have highly skewed, irregular or multimodal distributions:
In these instances, does it become more advantageous to use the median instead of the mean to infer properties of these distributions? Does it become less advantageous to use the mean in these examples?
Thanks
Whenever you compute a single real value that describes some aspect of a distribution ---whether this is the mean, mode, standard deviation, kurtosis, a particular quantile, or whatever--- that quantity measures what it measures and not what it doesn't measure. So the mean always measures the mean, irrespective of whether the distribution is unimodal, bimodal, trimodal, etc. Now, you ask whether the mean is good to "infer properties of these distributions". This begs the natural question, which properties? If the property of interest to you is the "centre" of the distribution, then obviously the mean will represent that property extremely well. On the other hand, if the property of interest to you is something else (e.g., the mode) then the mean might represent that very poorly.
All of this is just another way of saying that real quantities computed from distributions generally represent only one aspect of the distribution, and there is a loss of information when transitioning from the distribution to a descriptive quantity. So if you want to use descriptive quantities to represent properties of the distribution, you need to be specific about what properties are of interest to you. There is no single quantity (other than the distribution itself) that will give you "the properties" of the distribution.
Often the mean is of interest because often it relates to parameters of the underlying process that is described by the distribution.
This can also be true for skewed distributions like the Poisson distribution where the mean is equal to the rate parameter.
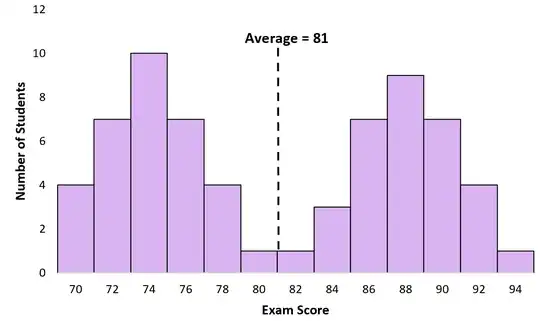
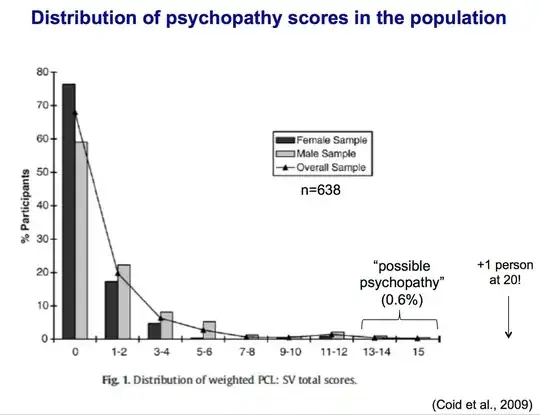
On the other hand, in the case of a bimodal or multimodal distribution you are often dealing with a mixture of distributions, each with their own mean. In that case the mean of the mixture is not a very useful descriptor that helps to understand the distribution.
A case that the mean might still be useful, even when it has little to do with the mechanics behind the process creating the distribution, is when the mean plays a role in the application.
For instance, if your application involves a sum of variables, then the distribution of the sum is of interest (and this will follow approximately a normal distribution with a single mode, centered around the mean).
Example: Say the distribution is for how much food to buy for the buffet on a cruise ship and the bimodal distribution describes the eating patterns of the individuals on a ship, then the distribution of the sum is of interest.
An example highlighting the difference between the two cases from the split in this answer are the different cost functions involved in optimization (one cost function for the fitting procedure, and one cost function as the actual optimization target). For instance, the mean might be desired for an application (e.g. it minimizes the squared error loss function) but the median of a sample from the distribution can be a better estimator of the distribution shape: http://stats.stackexchange.com/a/492143
An analogy with the usefulness of the mean to describe a distribution, when it is about the application, is the centre of mass in physics. Say you want to describe the motion of asteroid in the solar system then the exact shape of the asteroid is not much important and we make computations with the centre of mass. (there are some effects that make the shape a little bit important, e.g. tidal forces and radiation pressure). In the same way for statistics, the centre of probability mass (the mean) may not describe well the shape of some probability distribution, but it could be the only thing that matters in the application.
Your first plot shows a bimodal distribution that is close to symmetric, so it is quite likely that the mean would be close to or equal to the median. A mean or median is just a single number that summarizes some kind of information about the distribution. A single number will never tell you everything about the distribution, so it is hard to answer "how well" it works because the answer depends on what is important for you. It does not tell you anything about the multimodality, but neither would a median.
With your second plot, it is hard to say if the distribution is "irregular", or you just used the wrong parameters for the kernel density estimator. In kernel density estimation using a smaller bandwidth would always lead to curly shapes, while a high bandwidth would smooth such shapes more. The same applies to the histogram: with large bins it would be smoother, while with small bins. it would be a collection of peaks.
The third plot shows a skewed distribution. Again, choosing between mean and median would depend on what kind of information you want to summarize. The If mean is so sensitive, why use it in the first place? thread discusses in detail why we use means and what are the ideas behind that. TL;DR you actually may want the mean to be influenced by the extreme values, so it summarizes the "whole distribution" better.
There are many good answers here. I’ll just add here the general point to be made. You can summarise a distribution of values with a single number, the mean (or even two, say the standard deviation) but you always have to remember you are loosing information in doing so. That’s why you look at histograms before summarising.
So after looking at those histograms, you would
PS a better way for multimodal distributions would be to assume a parametric form for each component, and use maximum likelihood to estimate the relative components. But that’s likely an overkill in your case
A multi-model can be best explained by a localised distribution, but I don’t think there is any explicit localised distribution. Due to localised nature, spline regression or redial basis regression may help to model your problem.
