Covariate and Interaction Not Significant When Both in the Model

Question

I am looking at a survival model based on dosing variables, all of which are continuous. I have noticed when categorized, based on Kaplan Meier Curves, that low, medium, high doses behave differently, but the survival probabilities from least to greatest are high dose, low dose, medium dose. Thus, I created a variable DOSECAT with 3 levels (low, medium, high), and I expected an interaction with DOSECAT to be significant with DOSE. When DOSE, DOSECAT, and their interaction are all in a model together, DOSE and the interaction are both nonsignificant. However, if I remove one of them, the other is significant. What model do I use and/or how should this be interpreted?

proc phreg data=data;
CLASS DOSECAT/ PARAM=GLM;
model SURVIVALTIME*EVENT(1)= DOSE DOSECAT DOSE*DOSECAT; 
    HAZARDRATIO DOSECAT / DIFF=distinct;
    HAZARDRATIO DOSE / AT (DOSECAT=ALL);
run;

Answer 1

To address your scientific analysis question:

Although binning continuous data at an early stage of data exploration can make sense, binning generally shouldn't be used for statistical analysis. There are well-established ways to model a continuous predictor flexibly without binning in regression, including Cox regressions. My favorite is restricted cubic splines as implemented by rcs() in the R rms package, but a vignette shows how to use tools in the standard survival package to do that: with an example of a non-monotonic association with survival as you seem to have. I'm pretty sure SAS also provides that functionality, although I don't use it myself.

You can thus show continuous plots of association of dose with outcome. Depending on your audience you might want to display some categorical breakdown, but don't do that for analysis. As the categorical breakdown for Kaplan-Meier plots won't accommodate other predictors you might be modeling, I prefer to show example model predictions based on realistic combinations of predictors, with confidence limits.

To address your question about interactions:

As @whuber commented, loss of "statistical significance" when you add an interaction term is common. With small data sets, this could be something so simple as losing a degree of freedom to fitting the interaction term.

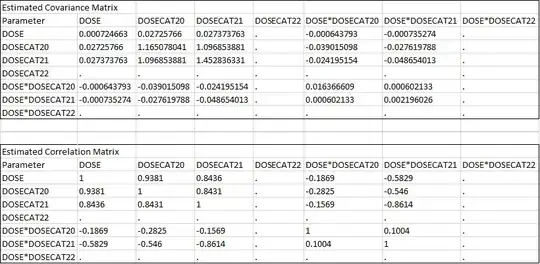
In your analysis of the full interaction model (leftmost table), there's probably an additional issue from the collinearity you have introduced. First, you introduced some collinearity by including both the dose and the dose-category even in the model without interaction (rightmost): dose-category is specified exactly by dose, so there's an inherent interdependence of those predictors. Then you compound that problem by multiplying the dose-determined dose-category by dose itself in the interaction term in the leftmost model.*

I suspect that the process has led to substantial collinearity in the model predictors, leading to high negative correlations among the coefficient estimates. Examine the coefficient covariance matrix. In that case neither dose nor the interaction might appear significant, but a combined Wald test on dose that includes both terms and thus takes the coefficient covariances into account might show that dose is "significant" overall.

Finally, your middle model has an interaction term without a term for dose itself. That's seldom a good idea. I'd recommend reading the extensive discussion on that page carefully, to understand why and how that might show up in apparent "significance." My guess is that your omitting a term for dose in that model minimized the collinearity and thus the high negative correlations among the coefficient estimates that otherwise made dose appear to lose "significance."

---

*I'm still not clear just what you were trying to model with this particular interaction term, but the principles I describe are generally applicable.