OLS uses t-test but GLM uses z-test in statsmodels python

Question

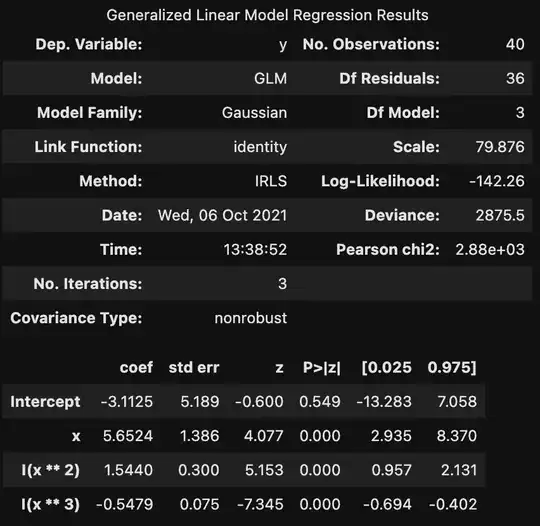
statsmodels library in python offers two different approaches for regression, ols and glm. While they are different methods, if the error is normally distributed, they should provide the exact same results (please see the code below).

However, one of the uses t-test and the other uses z-test. Consequently, the estimated confidence interval is different. We use t-test when sigma is not known and we estimate that based on the sample we have from the population. Can someone please explain why statsmodels.formula.api.glm uses z-test when family = sm.families.Gaussian()? Nowhere in the code we define sigma for the Gaussian distribution, so it is assumed to be unknown and we should estimate that using the sample observations we have. Considering that, we should use t-test then. Thank you

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import statsmodels.formula.api as smf
from statsmodels.stats.outliers_influence import summary_table
import scipy as sp
import math
from patsy import dmatrix
import scipy.stats
import statsmodels.api as sm



np.random.seed(seed=0)
Beg=-5
End=5
Samplingrate=40 #using more points, a more accurate spline can be generated
DrawingRate=100 #it is just for drawing the actual curve


#Data
#x
#xtrain=np.random.uniform(Beg,End,Samplingrate)   
x=np.linspace(Beg,End,DrawingRate)  
#y
#y=np.cos(x*np.pi/10 ) 
yactual=1+5*x+x**2-0.5*x**3
y=yactual+np.random.normal(loc=0.0, scale=10, size=DrawingRate)
#random selection
Selected=np.concatenate((np.ones(math.ceil(Samplingrate/2)),np.zeros(DrawingRate-Samplingrate),np.ones(math.floor(Samplingrate/2))),axis=None)
#np.random.shuffle(Selected)



#Traing Data
Data=pd.DataFrame({'x':x,'yactual':yactual,'y':y,'Selected':Selected})
Model2Ans=Data.copy()
Model3Ans=Data.copy()
DataTrain=Data[Data['Selected']==1]
DataTrain


#Model
DataTrain2=DataTrain.copy()
DataTrain3=DataTrain.copy()

Form='x+I(x**2)+I(x**3)'
model2   = smf.ols(formula = 'y ~ ' + Form,    data = DataTrain).fit()
model3   = smf.glm(formula = 'y ~ ' + Form,    data = DataTrain,family = sm.families.Gaussian()).fit()

DataTrain2['y_pred']=model2.predict(DataTrain2[['x','y']])
DataTrain2['y_error']=DataTrain2['y']-DataTrain2['y_pred']

DataTrain3['y_pred']=model3.predict(DataTrain3[['x','y']])
DataTrain3['y_error']=DataTrain3['y']-DataTrain3['y_pred']

print(model2.summary())
print(model3.summary())


predictions = model2.get_prediction(Data)
Model2Ans[['y_pred', 'mean_se', 'mean_ci_lower', 'mean_ci_upper', 'obs_ci_lower','obs_ci_upper']]=   predictions.summary_frame(alpha=0.05)
Model2Ans
#for glm
predictions = model3.get_prediction(Data)
Model3Ans[['y_pred', 'mean_se', 'mean_ci_lower', 'mean_ci_upper']]=   predictions.summary_frame(alpha=0.05)
Model3Ans

#Difference
Model2Ans[['y_pred', 'mean_se', 'mean_ci_lower', 'mean_ci_upper']]-Model3Ans[['y_pred', 'mean_se', 'mean_ci_lower', 'mean_ci_upper']]

I think you should rather raise an issue with statsmodel developers — seanv507, Oct 06 '21 at 20:42
I disagree with the close votes and see this as a statistics question, one that I find interesting and upvoted. // @seanv507 One of the `statsmodels` developers is on here and has responded to [a question of mine](https://stats.stackexchange.com/questions/457973/scale-in-logistic-regression). — Dave, Oct 06 '21 at 21:08
SimilarQs has been asked before, but maybe not in relation to statsmodel. See [Wald test in regression (OLS and GLMs): t- vs. z-distribution](https://stats.stackexchange.com/questions/56066/wald-test-in-regression-ols-and-glms-t-vs-z-distribution) and [what does the normality assumption in OLS and glm imply](https://stats.stackexchange.com/questions/489800/what-does-the-normality-assumption-in-ols-and-glm-imply) — kjetil b halvorsen, Oct 06 '21 at 21:43
As you (@kjetil-b-halvorsen) properly mentioned, the difference between the applications of t-test and z-test has been discussed before. However, I was not sure why statsmodels uses z-test not t-test. When we choose Gaussian, we usually do not know the variance of the population so t-test should be used. — smv, Oct 06 '21 at 23:40
@smv: Sure, but with glm's there is also the link function ... with a `gaussian` family and some non-`identity` link function, it is not obvious what is the right thing to do (are "mean" and "variance" still independent in this setting?) I am using R terminology, as I do not know abouts `statsmodel` — kjetil b halvorsen, Oct 07 '21 at 18:51

score 3 · Accepted Answer · answered Oct 06 '21 at 22:28

statsmodels does not change the distribution of the test statistic by family, nor whether the distribution is assumed to be correctly specified or not. GLM defaults to normal and corresponding chiquare distributions for Wald tests in GLM and in discrete models.

So, we only assume that the parameters are asymptotically normal distributed. Using t-distribution for Wald tests will often have better small sample behavior than the normal distribution, but that's mostly from Monte Carlo simulations and not a theoretical result.

However, statsmodels has an option use_t=True in fit(...) and changes the distribution used in Wald tests from z to t and chi2 to F.

The related option is whether to use robust standard errors, such as standard Huber-White sandwiches or cluster robust standard errors, which can also be chosen by a fit option, cov_type. Excess dispersion as in quasi-poisson is available by a scale option.

However, the default is to assume correctly specified likelihood.

The general approach is to provide accepted defaults for categories of models like GLM, but provide options for better small sample behavior or (somee) robustness to misspecification.

Aside, Wald tests are often liberal in small samples in GLM, while score tests can be conservative. Small sample corrections for Wald test go then in the wrong direction for score tests, especially robust score tests in analogy to the Huber-White robust Wald tests.

OLS uses t-test but GLM uses z-test in statsmodels python

1 Answers1