8

I recorded the length of 197 nursing care episodes. My normalised data $(x-\mu)/\sigma$ looks like this:

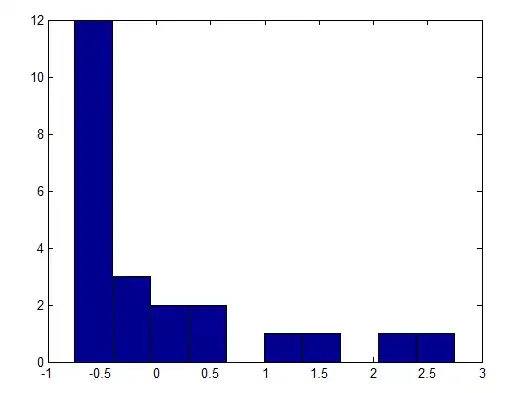
enter image description here

Kolmogorov-Smirnov gives me a p-value of 0.14. Can't be right surely?! Am I misinterpreting my results?

Nick Cox
  • 48,377
  • 8
  • 110
  • 156
HCAI
  • 737
  • 2
  • 7
  • 23
  • Uh, how do you know what $\mu$ and $\sigma$ are? – Glen_b Mar 30 '13 at 09:15
  • Re @Glen_b 's comment, perhaps you (User, not Glen) have confused $\bar{x}$ and $s$ with $\mu$ and $\sigma$ ? – Peter Flom Mar 30 '13 at 10:35
  • @Glen_b my $\mu$ is my sample mean. and my $\sigma$ is my sample variance. I agree Peter Flom, times are not possibly -ve, I wanted to apply this Smirnov test to rule out the use of one way ANOVA and hence opt for Kruskal-Wallis. Is this not a realistic approach? – HCAI Mar 30 '13 at 11:54
  • 2
    Sample mean and s.d. ($\bar{x}$ and $s$ ) are not population parameters ($\mu$ and $\sigma$). The Kolmogorov-Smirnov test is based on *known* distribution, not an estimated one, and the p-values aren't meaningful if you use parameter estimates. In particular, the p-values will tend to be larger. What you're doing is called a [Lilliefors test](http://en.wikipedia.org/wiki/Lilliefors_test), but you're using Kolmogorov-Smirnov tables... – Glen_b Mar 30 '13 at 11:59
  • are you dividing by s2? Should be s – user20650 Mar 30 '13 at 12:45
  • @user20650 yes my mistake. But even so why does the visual histogram conflict with the KS value? – HCAI Mar 30 '13 at 14:24
  • @Glen_b so I can just apply the Kruskal-Wallis test without `showing`that ANOVA is not appropriate due to normal property violation? – HCAI Mar 30 '13 at 14:26
  • Where's the conflict? First, @Glen_b appears to be correct about the misuse of the K-S test (I use "appears," instead of "is," only because we have to guess about some of the details of what you did). As a result, the p-value ought to be *much smaller* than reported. Consequently, you would quite definitely reject the assumption of a Normal distribution. But the histogram alone makes it abundantly clear that these data do not come from a Normal distribution! Everything is in good agreement. – whuber Mar 30 '13 at 15:24
  • @whuber I quite agree, I was expecting a much much lower p-value that's why I was surprised. In fact that value does not reject the H0 that it is normally distributed at even 10% – HCAI Mar 30 '13 at 15:28
  • OK, thanks for making that clear. (I had misread the ".14" as ".014", but no matter--it just makes your point even stronger.) Then @Glen_b has answered your question: the p-value is wrong because you used the sample moments in the calculation as if they had been known beforehand. – whuber Mar 30 '13 at 15:30
  • 1
    @whuber Would you pop that in an answer for me and I'll give you a thumbs up. So the truth is that the Lilliefors test is what's required not the KS test. Thank you – HCAI Mar 30 '13 at 16:31
  • Yes and no. The Lilliefors is the correct test to use if you want to do a K-S -style for normality but with estimated mean and standard deviation (though if testing normality is the aim, the Shapiro-Wilk or Shapiro-Francia tests are more typical and have better power). Here's the problem: that doesn't mean that a goodness-of-fit test addresses your original issue. You clearly carry the idea that the appropriate action when dealing with an ANOVA-like situation is to formally test normality via some goodness of fit test and only on rejection consider a nonparametric test. – Glen_b Mar 31 '13 at 01:11
  • 1
    However, the hypothesis test answers the wrong question; indeed a rejection answers a question you already know the answer to. To returns to your earlier question, you absolutely *can* just do a Kruskal-Wallis without testing normality. Only the fact that ANOVA is reasonably robust to mild non-normality makes it a reasonable choice in many circumstances. However, strong skewness does seem to be a weaker point for it, and if I anticipated skewness I'd very much lean toward not assuming normality (though Kruskal-Wallis is not the only option there). – Glen_b Mar 31 '13 at 01:12
  • @Glen_b Right I see. So once I've conducted this Kruskal Wallis test, what true value will I gain from going a post-hoc Mann-Whitney test between all groups? Let's say I have 5 groups of nursing data, I need to make 4! comparisons, surely this isn't quite right? – HCAI Mar 31 '13 at 07:57
  • I'm not sure what you mean by 'true value'. You do pairwise comparisons if you're interested in some or all pairwise comparisons. If no pairwise comparisons are of specific interest, then there'd be no benefit to doing them. – Glen_b Mar 31 '13 at 08:26
  • 1
    I am sort of confused as to why you are testing for normality here. If these are nursing care length, another way of looking at the times is time spent with patients. I would think that an exponential distribution would be more appropriate in this particular case. Have you read much about [Poisson Processes](http://en.wikipedia.org/wiki/Poisson_process#Definition)? – R S Mar 31 '13 at 23:08
  • @RS This is very interesting indeed! Infact I plotted a histogram of time (and another one of surfaces the nurse touched during each care episode) and fitted an expoential distribution. Contacts fit this very well, whereas the time has a lot of variation and therefore noisy. – HCAI Apr 03 '13 at 18:16
  • @HCAI Interesting example. Could you provide the data ? – Stéphane Laurent Aug 16 '13 at 22:19

1 Answers1

13

I think your issues are now clarified enough to construct a decent answer (with plenty of links explaining the issues).

There are several issues here:

1. K-S test with estimated parameters

The sample mean and s.d. ($\bar{x}$ and $s$ ) are not population parameters ($\mu$ and $\sigma$).

The calculation of the null-distribution (/critical values) of the Kolmogorov-Smirnov test is based on a fully specified distribution, not an estimated one -- the p-values aren't meaningful if you use parameter estimates. In particular, the p-values will tend to be larger than what you'd get if the conditions under which the test was derived held.

When you want to estimate parameters the Kolmogorov-Smirnov-type of test is called a Lilliefors test, which has different tables.

So the Lilliefors is the correct test to use if you want to do a K-S -style for normality but with estimated mean and standard deviation. It's not necessary to get the original paper to use this test - you can simulate the null distribution (and to substantially better accuracy than Lilliefors was able to do in the 1960s).

Though if testing normality is the aim, the Shapiro-Wilk or Shapiro-Francia tests are more typical and have better power; Anderson-Darling tests are also common (parameter estimation is an issue for the A-D test as well, but check the discussion of the issue in D'Agostino & Stephens' Goodness of Fit Techniques).

Also see How to test whether a sample of data fits the family of Gamma distribution?

However, having identified the issue with your p-value doesn't mean that a goodness-of-fit test addresses your original issue.

2. Using hypothesis testing of normality for procedures that assume it

You carry the idea that the appropriate action when dealing with an ANOVA-like situation is to formally test normality via some goodness of fit test and only on rejection consider a nonparametric test. I would say this is not generally an appropriate understanding.

First, the hypothesis test answers the wrong question; indeed a rejection gives an answer to a question you already know the answer to.

Is normality testing 'essentially useless'?

Testing normality

What tests do I use to confirm that residuals are normally distributed?

Is it reasonable to make some assessment of normality if one is considering using a procedure that relies on it? Certainly; a visual assessment - a diagnostic such as a Q-Q plot - shows you how non-normal your data appear and will let you see whether the extent and type of non-normality you have would be enough to make your concerned about the particular procedure you would be applying.

In this case your histogram would be enough to say 'don't assume that's normal', though ordinarily I wouldn't base such a decision only on a histogram

Secondly, you can just do a Kruskal-Wallis without testing normality. It's valid when the data are normal, it's just somewhat less powerful than the usual ANOVA.

Only the fact that ANOVA is reasonably robust to mild non-normality makes it a reasonable choice in many circumstances. If I anticipated more than moderate skewness or kurtosis I'd avoid assuming normality (though Kruskal-Wallis is not the only option there).

Khan and Rayner (2003),
Robustness to Non-Normality of Common Tests for the Many-Sample Location Problem,
Journal of Applied Mathematics and Decision Sciences, 7(4), 187-206

suggest that in situations of high kurtosis - when sample sizes are not very small - that the Kruskal Wallis is definitely preferred to the F-test* (when sample sizes are small they suggest avoiding the Kruskal-Wallis)

*(the comments apply to the Mann-Whitney vs t test when there are two samples)

You certainly don't need to show something isn't normal to apply Kruskal-Wallis.

There are other alternatives to the Kruskal Wallis that don't assume normality, such as resampling-based tests (randomization tests, bootstrap tests) and robustified versions of ANOVA-type tests.

Also see:

How robust is ANOVA when group sizes are unequal and residuals are not normally distributed?

3. Assumptions of ANOVA

ANOVA doesn't assume the entire set of numbers is normal. That is, unconditional normality is not an assumption of ANOVA - only conditional normality.

Which is to say, you can't really assess the ANOVA assumption on the original data; you assess it on the residuals.

https://stats.stackexchange.com/a/6351/805

https://stats.stackexchange.com/a/27611/805

Also:

https://stats.stackexchange.com/a/9575/805 (t-tests, a special case of ANOVA)

https://stats.stackexchange.com/a/12266/805 (regression, a generalization of ANOVA)

Community
  • 1
Glen_b
  • 257,508
  • 32
  • 553
  • 939
  • 1
    This is absolutely fantastic! Very thorough and succinct at the same time! Very much appreciated putting this matter to bed! – HCAI Apr 03 '13 at 18:19