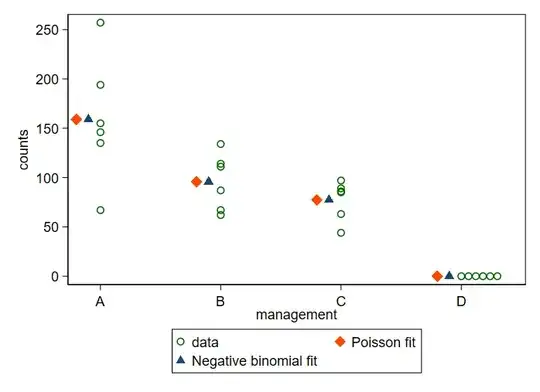
I have camera trap data for four different management types (A,B,C,D). I want to know whether there is an effect of these management types on the abundance of different mammalian herbivore species.
For some of the species, there are only zeros in one type of management, which complicates the analysis.
What do I do? I know I could do a Bayesian approach but before I go into that, I would like to know if there's a work-around that allows me to do this analysis using a frequentist approach.
The data for zebras:
counts <- (c(67, 194, 155, 135, 146, 257, 114, 134, 111, 87,
62, 67, 85, 89, 63, 86, 97, 44, 0, 0, 0, 0, 0, 0))
management <- rep(LETTERS[1:4], each = 6)
The model:
library(MASS)
model <- glm.nb(counts ~ management)
summary(model)
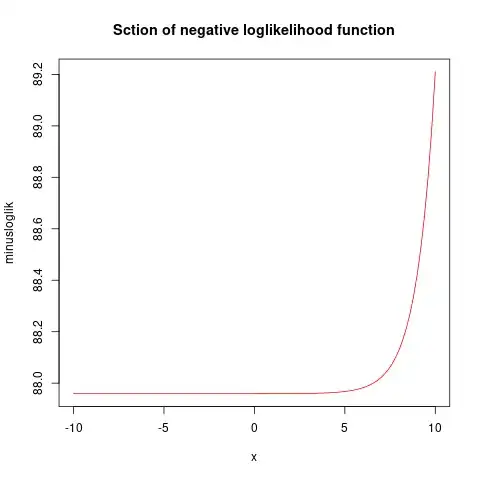
The output shows a huge standard error for group D, that only had 0s:
Call:
glm.nb(formula = counts ~ management, init.theta =
11.27380856,
link = log)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.42149 -0.35526 -0.00006 0.45934 1.70106
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 5.0689 0.1258 40.286 < 2e-16 ***
managementB -0.5063 0.1799 -2.815 0.00488 **
managementC -0.7208 0.1810 -3.982 6.84e-05 ***
managementD -25.3715 6344.9393 -0.004 0.99681
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for Negative Binomial(11.2738) family taken to be 1)
Null deviance: 339.360 on 23 degrees of freedom
Residual deviance: 18.139 on 20 degrees of freedom
AIC: 185.92
Number of Fisher Scoring iterations: 1
Theta: 11.27
Std. Err.: 4.11
2 x log-likelihood: -175.918
It can also not show me any differences between 'D' and all the other groups. pairwise comparison:
library(multcomp)
contrasts <- c(
"A - B = 0",
"A - C = 0",
"A - D = 0",
"B - C = 0",
"B - D = 0",
"C - D = 0")
H <- glht(model, linfct = mcp(management = contrasts))
summary(H)
Simultaneous Tests for General Linear Hypotheses
Multiple Comparisons of Means: User-defined Contrasts
Fit: glm.nb(formula = counts ~ management, init.theta =
11.27380856,
link = log)
Linear Hypotheses:
Estimate Std. Error z value Pr(>|z|)
A - B == 0 0.5063 0.1799 2.815 0.018355 *
A - C == 0 0.7208 0.1810 3.982 0.000271 ***
A - D == 0 25.3715 6344.9393 0.004 1.000000
B - C == 0 0.2145 0.1829 1.173 0.597425
B - D == 0 24.8652 6344.9393 0.004 1.000000
C - D == 0 24.6507 6344.9393 0.004 1.000000
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Adjusted p values reported -- single-step method)