Convolution between two random variables

Question

Given $X$ is a random variable which distributed uniformly in $[1,3]$ and $Y$ distributed uniformly in $[0,a]$. I need to calculate the value of the density function of:

$$Z=X+Y,$$

at a point $b$ (i.e., calculate $f_Z(b)$). I have some difficulties with the splitting of the integral with the bounds of $a$, $x$ and $b$.

Note: I don't know the bounds of $a$ and $b$ (these are not given).

See https://stats.stackexchange.com/questions/41467 for several completely different techniques to solve this problem. Consider first simplifying it a little by writing $X=1 + 2X_0$ and $Y=aY_0$ where $X_0$ and $Y_0$ are uniformly distributed on $[0,1]$ (and, presumably, independent). In these terms $Z=1+2X_0+aY_0.$ This suggests solving the slightly more general (but not any more difficult) problem of computing the density of $cX_0+aY_0$ for any positive numbers $c$ and $a.$ If you want to compute it using the convolution integral, then **draw a picture** of the integration region. — whuber, Sep 21 '21 at 12:55

score 5 · Answer 1 · answered Sep 22 '21 at 17:35

It's simpler to compute the distribution function

$$F_Z(b) = \Pr(Z \le b)$$

and then differentiate it, because (except where this function has cusps),

$$f_Z(b) = F_Z^\prime(b).$$

The level sets $Z=b$ are lines with slope $-1.$ Five of them are shown in this raster plot of $Z$ in a situation where $a\lt 2.$

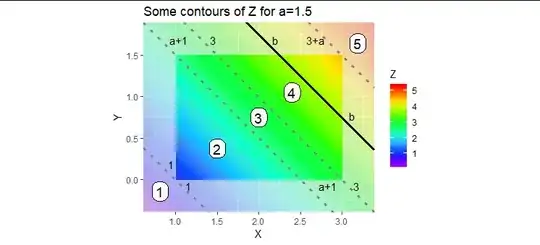
The solid line is the level set $Z=b$ (where $b$ is approximately $3.75,$ to illustrate). The region $Z\le b$ lies in the rectangle $[1,3]\times[0,a]$ (shown in bright colors) to the left and below the level set. Because the distribution of $(X,Y)$ is uniform,

$F_Z(b)$ is the relative area of the rectangle below and to the left of the line $X+Y=b.$

The dotted lines are special: they divide the plane into five regions, here numbered "1" through "5." The area below and to the left of the solid line in the figure consists of the part of region 2 in the rectangle--evidently the blue triangle; the part of region 3 in the rectangle--evidently the green parallelogram; and that portion of region 4 in the rectangle but below and to the left of the solid line--a green trapezoid. Therefore, $F_Z(b)$ in this example is the sum of those three areas, all divided by the area of the rectangle (equal to $2a$).

Use the area formulas of Euclidean geometry to finish the computation.

The picture when $a \gt 2$ looks a little bit different, so you might want to work that out separately.

There is a simplification.

It is geometrically obvious that the rate at which the area changes as $b$ is increased is proportional to the length of the level curve through $b$ lying in the rectangle. (It is straightforward to show this rigorously using the definition of the derivative.) The picture reveals that

As $b$ increases from $1$ to $a+1,$ the derivative increases in proportion to $b:$ it is linear.
As $b$ increases between $a$ and $3,$ the derivative remains constant.
As $b$ increases from $3$ to $3+a,$ the derivative decreases linearly, reaching $0$ when $b=3+a$.

Thus, the graph of $f_Z$ must have a trapezoidal shape between $b=1$ and $b=3+a.$

This observation determines $f_Z$ because that trapezoid must have unit area. To graph it accurately, draw any version of this trapezoid, compute its area $A$, then scale it in the $Y$ direction by a factor of $1/A.$

Here is the result for $a=3/2:$

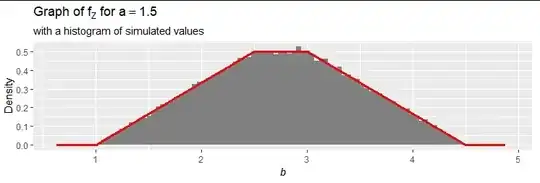
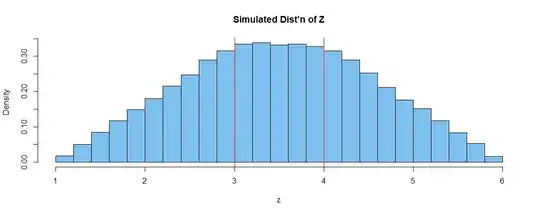
The calculation is supported by a simulation of 100,000 values of $Z,$ shown in the histogram.

score 2 · Answer 2 · answered Sep 21 '21 at 20:48

Graphical comment. Let $a = 3.$ A histogram of 100,000 simulated realizations of $Z$ suggests the shape of the density function of $Z.$

set.seed(921)
x = runif(10^5, 1, 3);  y = runif(10^5, 0, 3)
z = x + y
summary(z)

      Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
     1.009   2.735   3.498   3.500   4.268   5.992 

hist(z, prob=T, br=30, col="skyblue2", 
     main="Simulated Dist'n of Z")

Convolution between two random variables

2 Answers2