2

I am utterly confused. I have been reading about the optimality of Bayes classifier and Bayesian model averaging all the time, but when I try to dig deeper, I just get more confused.

On the one hand,

I have been hearing about the Bayes Optimal Classifier:

$$ y = \arg \max_{c_j \in C} \sum_{h_i \in H} P(c_j|h_i)P(T|h_i)P(h_i)=\arg \max_{c_j \in C} \sum_{h_i \in H} P(c_j|h_i) P(h_i|T) $$

Mitchell (1997) said that "no other classification method using the same hypothesis space and same prior knowledge can outperform this method on average." It also noted that the resulting hypothesis does not have to be in H. The above-cited Wikipedia article further said, "the hypothesis represented by the Bayes optimal classifier, however, is the optimal hypothesis in ensemble space (the space of all possible ensembles consisting only of hypotheses in H)."

Clarification

Through discussions with @tim, it became clear that there appear two different definitions of Bayesian Optimal Classifier. My use of the term above is a synonym of Bayesian Model Averaging, as noted by this paper. This seems how the term Bayesian Optimal Classifier is used in the above-cited sources, too. For example, Mitchell (1997) said of Bayesian Optimal Classifier that "no other classification method using the same hypothesis space and same prior knowledge can outperform this method on average." This implies that for his definition of BOC, the hypothesis space contains only some pre-determined hypotheses and may not contain the true hypothesis.

On the other hand,

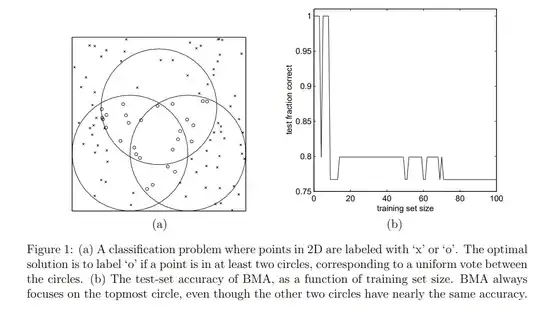
Minka (2002) gives an example where the simple average of three hypotheses outperforms Bayesian model averaging. In the below figure from the paper, the three circles represent the three hypotheses and the true class assignment is that an example is an "o" iff it is inside at least two circles.

enter image description here

Figure 1 (b) noted that the bigger the training set, the higher posterior probability it assigns to one of the circles (the top one), and the lower the accuracy.

His main point is that Bayesian model averaging assumes that exactly one hypothesis is responsible for all of the data and the posterior probability $P(h_i|T)$ only represents the uncertainty of which hypothesis generates the data. Even if the true hypothesis is not in $H$, as more data arrives, more and more weight will be given to the most probable hypothesis that is in H. By contrast, model combination such as bagging enriches the hypothesis space.

The view that Bayesian model averaging assumes data being generated by a single model seems to echo Bishop's Pattern recognition and machine learning.

But these points seem the opposite of what Wikipedia and Mitchell (1997) said about Bayes classifier.

Here is my question:

How do we understand the optimality of BMA/MOC? Specifically, statements like: - Mitchell (1997) page 175, "No other classification method using the same hypothesis space and same prior knowledge can outperform this method on average." - Wikipedia: "the hypothesis represented by the Bayes optimal classifier, however, is the optimal hypothesis in ensemble space (the space of all possible ensembles consisting only of hypotheses in H)?"

I have never seen proof of them. Also, the example in Minka (2002) cited above seems to have given a counterexample to both of these statements?

Tom Bennett
  • 677
  • 4
  • 15
  • 1
    Bayes optimal classifier is a theoretical concept. It assumes *knowing* the true distribution and maximizing it. It cannot be outperformed because in other cases you don’t know it and need to learn it from the data, hence are prone to being incorrect. – Tim Sep 18 '21 at 06:57
  • That is what I originally thought, from the proof on this page (https://en.wikipedia.org/wiki/Bayes_classifier), but I am confused by all this talk in Mitchell and the other Wikipedia page about the true hypothesis not having to be in the hypothesis space being considered. It feels like they are not talking about a theoretical concept. I also don't know if it will still be optimal when the true hypothesis is not in the hypothesis space. – Tom Bennett Sep 18 '21 at 07:07
  • 1
    What other Wikipedia page? Also if you ask about Bayes optimal classifier, why do you mention Bayesian model averaging? They are completely different things. – Tim Sep 18 '21 at 07:17
  • It is here (https://en.wikipedia.org/wiki/Ensemble_learning#Bayes_optimal_classifier). Specifically, I am confused about its claim that "Bayes optimal classifier is the optimal hypothesis in ensemble space," as the Minka paper seems to give a counterexample. I mention BMA because Bayes classifier seems also to weight $P(c_j|h_j)$ by the posterior $P(h_j|T)$ to get the combined classifier, just like BMA? Why are they completely different? Thanks – Tom Bennett Sep 18 '21 at 07:27
  • 1
    Have a look at https://esajournals.onlinelibrary.wiley.com/doi/abs/10.1002/ecm.1309 – Florian Hartig Sep 22 '21 at 07:26

1 Answers1

1

Bayes optimal classifier assumes that you know the true distribution. The predictions are optimal because you do the maximization in terms of the true distribution. In any other case, you don't know the true distribution, you need to learn or approximate it, hence no classifier can be better. The classifier is not concerned about the true hypothesis not being in $H$, because, by definition, the true hypothesis distribution is $H$.

Bayesian model averaging averages different models according to their posterior probabilities. Posterior probabilities are estimated from the data and the prior. Here we are talking about distributions that are estimated, rather than known. It cannot be better than the Bayes optimal classifier, because at best it could learn the distribution exactly and achieve the same performance.

There are many things with "Bayesian" in their names, for example, naive Bayes classifier, Bayesian statistical models, Bayesian networks, Bayesian neural networks, etc, that have in common that they somehow use probabilistic models and Bayes theorem, but have nothing to do with Bayes optimal classifier.

Tim
  • 108,699
  • 20
  • 212
  • 390
  • I don't get "by definition, the true hypothesis distribution is H." The hypothesis space matters. In Minka's example, if we plug in the theoretical posterior probabilities instead of learning them from data, we will still give all the weight to the top circle, and thus underperform taking an equal average of the three hypotheses. For Bayes classifier to be optimal, we need the true P(Y|X) but what we get is P(Y|X,H)=∑hP(Y|X,h)P(h), and it is only when the true hypothesis is in H do we have any hope to get P(Y|X)=P(Y|X,H) even if we know all the probabilities. – Tom Bennett Sep 18 '21 at 14:27
  • The other thing I realized is that there are slightly different definitions of Bayes Classifier. On the one hand, [Wikipedia](https://en.wikipedia.org/wiki/Bayes_classifier) defines it exactly like the entry you cited, i.e., it assumes we know $P(Y|X)$, On the other hand, the other [Wiki entry](https://en.wikipedia.org/wiki/Ensemble_learning#Bayes_optimal_classifier) and Mitchell (1997) p175-176 defines it to be weighted by the posterior: $\arg \max_{v_i \in V} P(v_i|h_i)P(h_i|D)$, though these probabilities are not learned. It says what is optimal for the given data and hypothesis space – Tom Bennett Sep 18 '21 at 14:59
  • @TomBennett if they are given they are known. A classifier is Bayes optimal if it has the properties. *The* Bayes optimal classifier is one that knows the true probabilities. – Tim Sep 18 '21 at 15:25
  • Many thanks for clarifying. For Minka's example, if we plug in the theoretical probabilities (which can be figured out because it is an artificial example), it will have the properties and be Bayes optimal, according to the claims of [Wikipedia](https://en.wikipedia.org/wiki/Ensemble_learning#Bayes_optimal_classifier), but it will clearly underperform equally averaging the 3 hypotheses, because the true hypothesis is not in the space. Isn't that still odd? – Tom Bennett Sep 18 '21 at 17:41
  • @TomBennett not sure what do you mean. Optimal Bayes classifier *knows* the whole hypothesis space and the associated probabilities. – Tim Sep 18 '21 at 17:48
  • Thanks. I think I know my exact confusion - [Wikipedia](https://en.wikipedia.org/wiki/Ensemble_learning#Bayes_optimal_classifier) states that the hypothesis represented by the Bayes optimal classifier does not have to be in H, but is the optimal hypothesis in the ensemble space. (Mitchell said almost the same thing.) But Minka's example seems to show that the hypothesis constructed using the same formula may underperform the simple average of hypotheses, when the true hypothesis is not directly in H but is the linear combination of them. These statements seem contradictory. – Tom Bennett Sep 18 '21 at 18:08
  • I found [another paper](https://web.cs.ucdavis.edu/~davidson/Publications/ModelAve.pdf) that says Bayes Optimal Classifier and Bayesian Model Averaging are the same. The statistics literature calls BMA the ML literature tends to call it BOC. BOC used in this sense is how my question and the cited sources used it. It does feel different from the "everything is known" BOC definition, which I also often see. Maybe the term is overloaded. Getting more confused :-) My question that Minka's example seems to contradict the BOC being the optimal hypothesis in the ensemble hypothesis space remains. – Tom Bennett Sep 19 '21 at 01:57