2

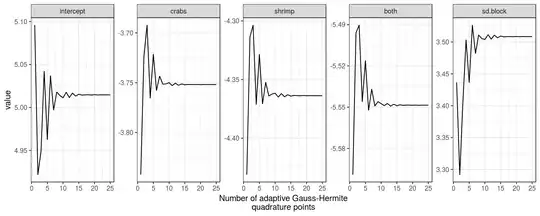
According to the documentation for glmer, nAGQ refers to "the number of points per axis for evaluating the adaptive Gauss-Hermite approximation to the log-likelihood". I understand the n in the acronym stands for number of points, while the AGQ stands for Adaptive Gauss-Hermite Quadrature.

Douglas Bates further explains that the difference between nAGQ=0 or nAGQ=1 "is whether the fixed-effects parameters, $\beta$, are optimized in PIRLS or in the nonlinear optimizer."

The general advice seems to be that setting nAGQ = 0 is less accurate than setting nAGQ = 1 (the default), and that where possible setting it higher is better still, although there will be a tradeoffs inasmuch as higher values of nAGQ will have longer runtimes and a higher chance of convergence failures.

I have in mind scenarios in which the person running the model intends for the results to be published in a scientific paper, and not scenarios in which the person doesn’t care much about accuracy as opposed to runtime. Is setting nAGQ = 0 only appropriate when the model will otherwise not converge (or won't converge in sufficient time), and all other means of resolving the convergence issue have failed? What other factors make it more or less acceptable?

Robert Long has suggested elsewhere on this site that

You might get more accurate results with nAGQ>0. The higher the better. A good way to assess whether you need to is to take some samples from your dataset, run the models with nAGQ=0 and nAGQ>0 and compare the results on the smaller datasets. If you find little difference, then you have a good reason to stick with nAGQ=0 in the full dataset.

This seems a good rule of thumb, although there remains the question of what to do if the subsampled data has convergence failures when nAGQ is greater than 0.

My question is related to another question, in which I could not find any other way to make a model converge aside from setting nAGQ = 0, and usually had convergence failures on subsampled data.

user1205901 - Reinstate Monica
  • 11,303
  • 26
  • 77
  • 152

1 Answers1

1

I would saying nAGQ = 0 is acceptable when it's "good enough", e.g.

  • you simply can't get the model to perform adequately with nAGQ > 0 (although I would be highly suspicious of this case; it would be better to fix the problem and/or use multiple optimizers (via allFit()) to confirm that the fit with nAGQ ≥ 1 is actually getting an adequate fit).
  • Using nAGQ >0 is computationally infeasible. (glmmTMB may be faster, especially if there are many top-level (variance/covariance + fixed-effect) parameters, although it can only handle nAGQ=1 (i.e. Laplace approximation); MixedModels.jl is likely to be fast as well. GLMMadaptive does nAGQ>1, but I don't know about is speed.)
  • You have tested on similar cases where both nAGQ=0 and nAGQ=1 work and found that nAGQ=0 is generally close enough for your purposes (this is a scientific, not a statistical, criterion). There is an example here:

graph of dependence of estimated values on AGQ

The best description I have found of the profiling assumption is in section 16.2 of the TMB documentation, which states that "one can apply the profile argument to move outer parameters to the inner problem without affecting the model result" when these assumptions hold:

Assumption 1 The partial derivative $\partial_\beta f(u,\beta, \theta)$ is a linear function of $u$.
Assumption 2 The posterior mean is equal to the posterior mode: $E(u|x)=\hat u$

They hold exactly for linear mixed models. It's hard to guess exactly when they are likely to hold, but I would very tentatively speculate that (1) will be OK when the inverse link function is "not too nonlinear", i.e. when the linear predictors are mostly in a range where the second derivative of the inverse link function is small (e.g. for a logit link, values near zero) and (2) will be OK when the "effective sample size" per group is large so that we can wave our hands in the direction of the Central Limit Theorem (e.g. binomial observations with $\textrm{min}(pN, (1-p)N)$ not too small, or Poisson observations with average counts not too small — these are also the cases where penalized quasi-likelihood is likely to be OK, see Breslow 2003).

But, I'm not aware of a systemic exploration of these issues.

Breslow, Norm. “Whither PQL?” UW Biostatistics Working Paper Series, #192, xx xx 2003. http://www.bepress.com/uwbiostat/paper192.

Ben Bolker
  • 34,308
  • 2
  • 93
  • 126