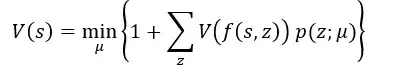I want to formulate a game of darts as a dynamic program. The goal is to minimize the number of darts thrown while reaching checkout. A dart player has a score s. If his score is s = 2, there is only a single legal / possible move.
- He can checkout by throwing at
D1 - Every other action is not legal and results in a so-called bust and the score remains the same, s =
2
The above can be formulated as:
Now I write the Bellman equation as:
Where mu is the aiming location on the dartboard. The reward is equal to 1 (one dart thrown). In addition, we have the probabilities of reaching s_i+1 when aiming at mu and the corresponding value function of s_i+1. The terminal condition V(0) is equal to 0
So, inserting all for s = 2, excluding the illegal moves, leads to the following:
V(2) = min{1 + (V(0) * p(D1;mu))
Lets assume there are two possible values for mu, namely the center of D1 and the center of D19, which is on the opposite of the dartboard. Logically
p(D1, center D1) > p(D1, center D19)
However, V(0) = 0, so
p(D1, center D1) * V(0) = p(D1, center D19) * V(0) = 0
So, if we want to minimize the Bellman curve, there is no optimal solution. Both options lead to the same result, V(2) = 1. However, logical reasoning would suggest aiming for mu = center D1 is the optimal / desired solution. What am I doing wrong here?
So, I thought maybe I should add the illegal moves into the Bellman equation. This would look as follows:
V(2) = min{1 + sum((V(0) * p(D1;mu)) + (V(2) * p(S1;mu)) +
(V(2) * p(S2;mu)) + ... + (V(2) * p(T19;mu)) + (V(2) *
p(T20;mu)))
However, now there is a circular reference. How should this be addressed? Should the illegal moves be added? Please help me explain what I am doing wrong.