1

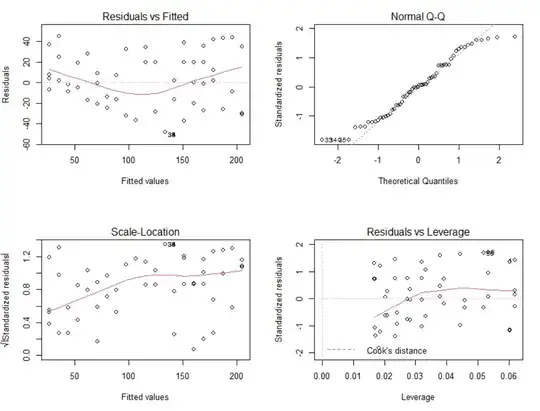
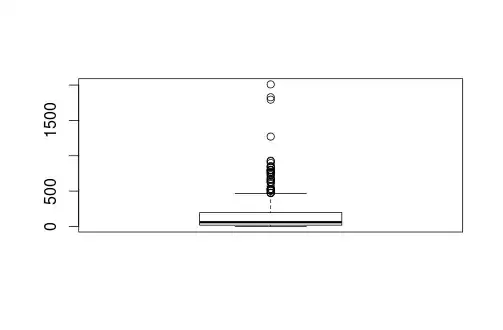
Is this simple linear regression a good fit? Are there any transformations that would improve it?

The data is discrete interval count vs discrete interval count (the count of steps walked per time)

  • Variables: time spend walking ~ steps walked
  • Dependent: time spend walking
  • Explanatory: steps walked

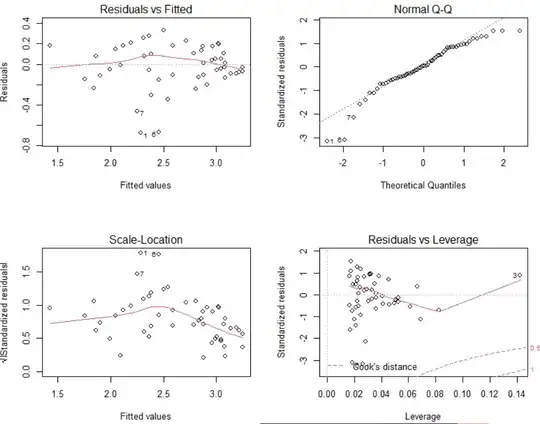
without log transform enter image description here

with log transform on explanatory

enter image description here

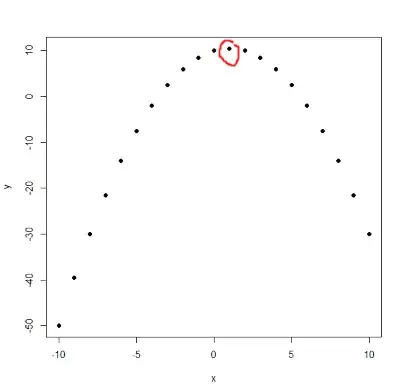
with log transform on dependent enter image description here

with log transform on dependent and explanatory

enter image description here

Adrià Luz
  • 746
  • 11
Michael Latter
  • 11
  • 2
  • 2
    What are your data? What are your variables? How many explanatory variables are there? What are you hoping to accomplish with this model? Etc. – gung - Reinstate Monica Sep 14 '21 at 00:55
  • QQ plot shows normality assumption may be violated (a bit heavy in the tails), and Residual vs Fitted plot gives some evidence that linearity assumption may be violated. A log transformation on the explanatory may improve your linearity, and a log transformation on the dependent may improve normality. My advice is to start with the linearity as that may solve the normality. – jros Sep 14 '21 at 15:00
  • @jros added those log transforms. It appears linearity was fixed by a log transform on both. Log transform on both does seem to fatten the tails, I am not sure of the implications of this. – Michael Latter Sep 15 '21 at 06:27
  • See https://stats.stackexchange.com/questions/58141/interpreting-plot-lm/65864#65864 – Tim Sep 15 '21 at 07:20
  • 1
    You've missed out the most basic graph of all: a scatter plot of time versus steps with fitted line superimposed In this example, I'd be concerned with whether a fitted function should respect the origin 0 steps, 0 time. – Nick Cox Sep 15 '21 at 09:10
  • 1
    This should be about the substance as well as the statistics. On the face of it time and steps should be proportional as a good first approximation. But people get tired etc. and so I would expect some curvature. And there is nothing here about whether your data are heterogeneous because of mixing different people and/or different conditions. – Nick Cox Sep 15 '21 at 09:34
  • Alone the lines of what @NickCox said, this does not seem to be a place for statistical inference but rather a place for description. The relationship can be described with a _loess_ nonparametric smoother and with quantile regression, the latter giving risk to, for example, 3 curves estimating 3 quartiles. You might repeat the analysis using x=steps y=time per step. – Frank Harrell Sep 15 '21 at 11:16

0 Answers0