Discrete and Continuous variables. What is the definition?

Question

The definition of a continuous variable in our class seems to be, well, not a definition, as there are exceptions not included in its definition.

I am a 4th year math student and find it appalling that such a rinky dink thing can be a definition. Could someone possible give me a definition that is capable of differentiating between continuous variables and discrete ones that is completely accurate or give me a list of all the continuous variables that need to be treated as discrete and when. So far I have that money is somehow discrete as well as time sometimes?

Concentrations I'm not sure about (e.g parts per million) but weight, length and temperature seem to be continuous. Time seems to be completely confused.

They claim that a continuous random variable is one that would take an infinite amount of time to list all possible values, whereas a discrete one is one that can be counted.

Answer 1

A random variable $R$ is said to be continuous if for every real number $t,$ the probability that $R$ equals $t$ is zero $P(R = t) = 0.$ A random variable $R$ is said to be discrete if there exists a countable set of values $t_1, \ldots, t_n, \ldots$ such that $P(R = t_i) > 0$ for all $i$ and $\sum\limits_i P(R = t_i) = 1.$ The Radon-Nikodym and Lebesgue Decomposition theorems show every the cumulative distribution function (a.k.a. CDF) of every random variable can be expressed as $$ F = aF_{ac} + b F_{dc} + c F_{pm} $$ where $a, b, c \geq 0$ and $a + b + c = 1,$ where $F_{ac}$ is the CDF of an absolutely continuous random variable (i.e. $F_{ac}$ admits a density), and $F_{dc}$ is the CDF of degenerated continuous random variable and $F_{pm}$ is the CDF of a discrete random variable (so pm stands for point-mass). It is hard to construct examples of degenerated continuous random variables for their CDF must be continuous, increasing, not constant, and have a zero derivative almost everywhere. A typical example is Cantor's Devil Staircase function (https://en.wikipedia.org/wiki/Cantor_function). So you usually assume that random variables are either absolutely continuous, discrete or mixture of these two types.

EDIT: this question received a lot of attention, so let me expand a bit. This definition is motivated on the 1D case (univariate random variables). The condition that $P(R = t) = 0$ for all $t$ signifies that the CDF of $R$ is a continuous function $\mathbf{R} \to [0,1].$ Indeed, it is a well-known fact that a CDF is non-decreasing function, a fortiori it can only have jump discontinuities. But a jump discontinuity of a CDF is precisely at the "atoms" of the distributions (an "atom" of a random variable $R$ is a value values $t$ such that $P(R = t) > 0$). To see this, we use that the CDF $F$ is already (by definition) continuous on the right, so that $F$ is continuous if and only if is continuous on the left. Now, $$ F(t) - F(t - \delta) = P(R \leq t) - P(R \leq t - \delta) = P(t - \delta < R \leq t), $$ by measure-theoretic properties of $P,$ the right hand side converges to $P(R = t),$ so that $F$ is continuous on the left if and only if $P(R = t) = 0,$ which is the main motivation to call an atomless random variable a "continuous random variable."

Answer 2

A random variable is a function that maps a sample space to the real numbers. A continuous random variable is such a function such that it can take on any value in an interval - not any arbitrary interval, but an interval which makes sense for any particular random variable under consideration. A discrete random variable is a random variable that can only assume a finite or countably infinity number of distinct values.

For reference, see Mathematical Statistics with Applications, 5th Ed., by Wackerly, Mendenhall, and Scheaffer. The random variable is defined as Definition 2.11 on p. 65. The discrete random variable is defined as Definition 3.1 on p. 76. The continuous random variable is defined on p. 136.

In the referenced textbook, I have never seen exceptions to these definitions, except perhaps the so-called "mixed" random variables that are partly discrete, partly continuous.

Answer 3

Supplemental to answers of @WillM and @AdrianKeister, both (+1).

Sometimes we model essentially discrete situations as continuous. If you want to be fussy about amount of debt on individual credit cards in the US, then that debt is truly discrete at the one cent level. Even interest charges will be rounded to the nearest cent. But if a continuous model such as $\mathsf{Norm}(\mu = 10000, \sigma=2000)$ is approximately correct for a particular group of cardholders, that is easer to deal with than a discrete random variable with something like $1\,200\,000$ discrete values spaced 1-cent apart.

Also, it is common to approximate $\mathsf{Binom}(n=100, p-1/2)$ as $\mathsf{Norm}(\mu=50, \sigma=5).$ Even though this is perhaps done less frequently now that we have software that deals gracefully with 101 discrete outcomes. The probability of getting between 45 and 55 (inclusive) heads in 100 independent tosses of a fair coin is exactly $0.72875$ to five places--in R using the CDF pbinom or the PDF (PMF) dbinom.

diff(pbinom(c(44,55), 100, .5))
[1] 0.728747
sum(dbinom(45:55, 100, .5))
[1] 0.728747

A normal approximation, using the 'continuity correction', is $0.72867$ to five places. In practical terms, it would take an enormous number of coin tosses to distinguish between the two answers.

diff(pnorm(c(44.5, 55.5), 50, 5))
[1] 0.7286679

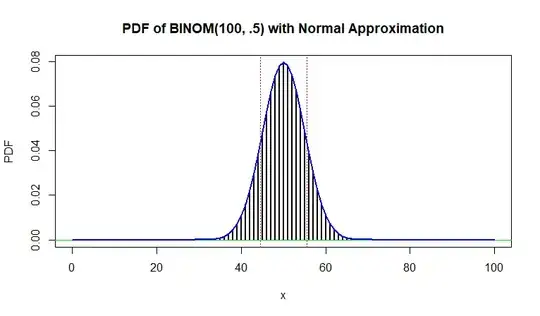
R code for figure:

x = 0:100; PDF = dbinom(x, 100, .5)
hdr="PDF of BINOM(100, .5) with Normal Approximation"
plot(x, PDF, type="h", lwd=2, main=hdr)
abline(h=0, col="green2")
curve(dnorm(x, 50, 5), add=T, col="blue", lwd=2)
abline(v=c(44.5, 55.5), col="red", lty="dotted")

Formally, working below the measure-theoretic level, a continuous random variable can be defined in terms of its density function. [WMS 6e, p155], which has $f(x)\ge 0,$ for real $x,$ with $\int_{-\infty}^\infty f(x)\,dx = 1.$ Probabilities are defined for intervals $[a,b],$ with $a\le b$ as $\int_a^b f(x)\,dx,$ with the consequence that the probability of any single point is $0.$

Answer 4

Not all physical phenomena are strictly discrete or continuous. Some are obvious, like number of children. But "continuous" has more to do with convenience and physical processes rather than a be-all-end-all data dictionary. For instance, weight can be rounded to the nearest tenth, or hundredth, down to the actual sensitivity of the instrument used to measure weight; it remains discrete in the sense that you can enumerate the possible values starting with 0.0, 0.1, 0.2, ..., but it's also continuous in the sense that theoretically it makes sense to consider weight as real valued. (As a 4th year maths student, you can appreciate that the rationals are dense in the reals, and those are countable.)

The designation (discrete vs. continuous) only matters when you assign a probability model to those values. Ideally, the choice of model is somewhat justified by the physical, random process giving rise to the values. For instance, if you assume the arrivals of cars over a segment of highway are of constant intensity, and independent in inter-arrival times, you can consider a Poisson counting process to estimate the probability of a certain volume of traffic at a particular time. Interestingly, Quetelet developed the BMI because the distribution looked normal, but modern biometricians suggest that we should have created a metric based on dividing by height cubed as it would represent a weight density, rather than surface area. Not withstanding, weight (or mass index) makes sense as a continuous value any way you cut it.

Answer 5

Here is the most elementary definition I can think of.

If $X$ is a random variable then it has a "distribution function", also known as as CDF. If we let $F(t)$ denote the distribution function then by definition $F(t) = P(X\leq t)$. If this distribution function is continuous (as a function in ordinary calculus) then we say that $X$ is a continuous random variable.

We say that $X$ is a discrete random variable if the "support of $X$" consists of the integers. Recall the "support of a random variable" is the set of possible values the random variable may take. Let us denote the support by $\text{supp}(X)$. Therefore, we say that $X$ is a "discrete random variable" if $\text{supp}(X)\subseteq \mathbb{Z}$. Even more simply, we say $X$ is discrete if the value of $X$ is always some integer value.

Note, the above definition for "discrete" is not the most general definition, but as an initial definition it is good enough. The most important discrete random variables are integer valued anyway. Hence you do not need to be concerned about (yet) what it means to be a "countable set" at the moment.

If $X$ is a discrete random variable then its CDF will look like a staircase, the CDF will be piecewise constant.