p-value and its application in Hypothesis Testing

Question

Background

It looks p-value is not easy to understand and there are few people who are able to explain in a simple intuitive manner. After having watched YouTube and read articles, still not sure what p-value is.

• Not Even Scientists Can Easily Explain P-values

To be clear, everyone I spoke with at METRICS could tell me the technical definition of a p-value — the probability of getting results at least as extreme as the ones you observed, given that the null hypothesis is correct — but almost no one could translate that into something easy to understand.

It’s not their fault, said Steven Goodman, co-director of METRICS. Even after spending his “entire career” thinking about p-values, he said he could tell me the definition, “but I cannot tell you what it means, and almost nobody can.” Scientists regularly get it wrong, and so do most textbooks, he said. When Goodman speaks to large audiences of scientists, he often presents correct and incorrect definitions of the p-value, and they “very confidently” raise their hand for the wrong answer. “Almost all of them think it gives some direct information about how likely they are to be wrong, and that’s definitely not what a p-value does,” Goodman said.

• Practical Statistics for Data Scientists
  
  

Objective

To build the understanding about p-value by trying and error, I like to get feedbacks on what is fundamentally wrong in my understanding below if any.

Criteria $\alpha$ for Highly Unlikely

It is subjective but we can regard 2.5%chance for an event to happen as "highly unlikely" for directional-one-tailed situation. Likewise 5% for two-tailed non-directional. Then we use it as the criteria $\alpha$ to decide if an event is an extreme case.

p-value

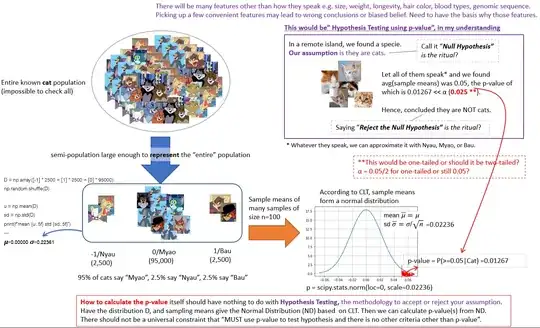
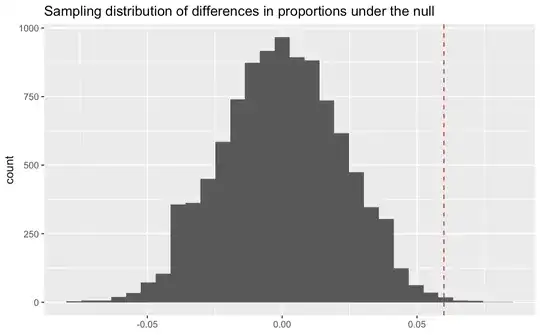
Suppose there is a distribution D of sampling means of the word cats spaek. 0 for myao, -1 for nyau and 1 for bau. The area of D is normalized to 1 so that a probability can be calculated by the size of an area in D.

The probability where a sample mean $\overline {x} \ge 0.05$ would be $P( \ge 0.05 | D)$. This is the p-value and it is 1.27% by calculating the area in D.

I like to clarify that Calculating p-value as a probability is one thing, but Comparing p-value with $\alpha$ to test a hypothesis is another. p-value is calculated from D and the sample mean $\overline {x}$. Either use it to test the hypothesis or not is a different matter.

The articles and YouTube videos I saw always started with Null Hypothesis but how to calculate p-value can be explained regardless with using it in hypothesis testing.

Using p-value for Hypothesis Testing

Now we have discovered a new island and found a specie that speaks the words myao, nyau and bau. So we put a hypothesis $H_0$ that they are cats. We let them speak and collect the words they said, and the mean was 0.05. The p-value is 1.27%.

As we established, less than $\alpha$ (2.5%) is an extreme case to happen. Hence we will say they are not cats (reject $H_0$).

$\alpha$ as False Negative Rate in Hypothesis Testing

Even if we take samples from cats, there is a chance when all or most of them say bau. Then the p-value for the sample mean will be $< \alpha$ and we will say they are not cats, which is false negative. Hence the $\alpha$ is the False Negative rate we accept.

Answer 1

I think you'll find this helpful, particularly re: all your questions about p-values in the context of hypothesis testing.

When it comes to actually understanding what p-values are (beyond the standard definition, which you've already stated), I always find it useful to run a little simulation. In this case, I believe using a non-parametric method such as a permutation test helps with the intuition. You can find a high-level overview of permutation tests in Practical Statistics for Data Scientists.

Imagine we've run an A/B test on our website. The test consists in changing the colour of the "Buy now" button from blue to green. Our (alternative) hypothesis is that the green colour will increase the rate at which users who visit the page click on the button. Therefore, $$ H_0: p_{\operatorname{green}} = p_{\operatorname{blue}} \\ H_1: p_{\operatorname{green}} > p_{\operatorname{blue}} $$ where $p_c$ is the proportion of users who click on the "Buy now" button after visiting the page, for $c\in\{\text{green}, \text{blue}\}$.

Note this is equivalent to testing: $$ H_0: p_{\operatorname{green}} - p_{\operatorname{blue}} = 0 \\ H_1: p_{\operatorname{green}} - p_{\operatorname{blue}} > 0 $$

Now, let's assume we've collected the test data ($N=1500$) and we see that: $$ p_{\operatorname{green}} = 0.26 \\ p_{\operatorname{blue}} = 0.20 \\ p_{\operatorname{green}} - p_{\operatorname{blue}} = 0.06 $$ That is, 26% of users in the treatment group (green colour) clicked on the button and 20% of users in the control group (blue colour) clicked on the button. The difference in proportions is 0.06 (6 percentage points).

Now, the main idea of a permutation test is to simulate the distribution of the difference in proportions if the null hypothesis were true. In other words, if the colour of the button made no difference ($H_0$ true), what kinds of differences in proportions could we expect to see by chance alone?

The algorithm works as follows:

1. Combine the results from the different groups in a single data set
2. Shuffle the combined data, then randomly draw (without replacing) a resample of the same size as group A
3. From the remaining data, randomly draw (without replacing) a resample of the same size as group B
4. Whatever statistic or estimate was calculated for the original samples (e.g. difference in group proportions), calculate it now for the resamples, and record; this constitutes one permutation iteration
5. Repeat the previous steps $R$ times to yield a permutation distribution of the test statistic

We can simulate the test data and visualise the two proportions as follows:

set.seed(122)
# note 0.25 and 0.19 are the true population proportions
# but the sample proportions are 0.26 and 0.20 as stated above
test_data <- tibble(
  colour = factor(rep(c('green', 'blue'), each = 750)),
  clicked = as.integer(c(rbernoulli(750, 0.25),
                         rbernoulli(750, 0.19)))
)

test_data %>%
  group_by(colour) %>% 
  summarise(proportion = mean(clicked)) %>% 
  ggplot(aes(x = colour, y = proportion, fill = colour)) +
  geom_col(fill = c('deepskyblue', 'aquamarine3'))

Now let's run the permutation test 10,000 times:

R <- 10000
n_green <- 750
n_blue <- 750
N <- n_green + n_blue
click_data <- test_data %>% 
  pull(clicked)

random_diffs <- c()

for (i in 1:R) {
  green_idx <- sample(1:N, n_green, replace = FALSE)
  blue_idx <- setdiff(1:N, green_idx)
  diff_in_props <- mean(click_data[green_idx]) - mean(click_data[blue_idx])
  random_diffs <- c(random_diffs, diff_in_props)
}

We have just calculated 10,000 differences in proportions under the assumption that the null hypothesis is true (because we have completely ignored the colour of the button). Now we can plot the histogram of these differences - this is the sampling distribution of our test statistic under the null hypothesis:

tibble(
  differences_under_null = random_diffs
) %>% 
  ggplot(aes(x = differences_under_null)) +
  geom_histogram() +
  geom_vline(xintercept = 0.06, color = 'brown3', linetype = 'dashed') +
  labs(title = 'Sampling distribution of differences in proportions under the null',
       x = NULL)

Here, the red line represents the actual difference we observed in our test (0.06). The p-value is the probability of observing a difference at least as extreme as the one we observed in our test (0.06), if the null hypothesis were true. Hence, the p-value is simply the proportion of random differences from our permutation test that are bigger than 0.06:

mean(random_diffs > 0.06)
[1] 0.0022

The p-value is 0.0022 (or 0.22%), which is < 0.01 and so we would conclude that there's strong evidence against the null hypothesis, we would reject it, and we would roll out the green button to 100% of web traffic.