Neural network fails to learn regression task when inputs are generated from a simple analytical function

Question

Problem discription

I have a forth order polynomial function clearly defined. I would sample $n$ number of points and feed them to my function to get the corresponding $y$ values. I then apply a FC neural network to learn this function, which I presume should be quite a simple task.

When I perform random sampling from the input space, the neural network learns just fine. I can see the training loss getting smaller and in just a few epochs, gets pretty close to 0. Now, I change my sampling method to a special sampling method that I have, and repeat the same process. Suddenly the NN seems to not learn the function at all. And I don't mean it's generalizing poorly at the test set, it's not fitting to the training set. The loss training loss stays stagnant every epoch.

This is extremely perplexing to me. The NN learns just fine when the inputs are sampled randomly, but fails completely when another set of inputs which I generated using alternative method was used. When I examine the predicted values from the model, it seems it's predicting everything with just the same output value. This was not the case when it trained on random generated input.

Properties of the problematic data

I tried to do a tSNE on my problematic input data, and color them by y value. The low and high values seems to seperate themselves pretty well in this space, so I don't see why the NN just can't learn it properly.

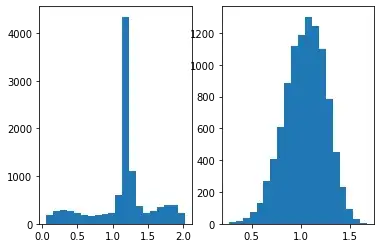
Per Davidmh's suggestion, I looked at a histogram of the y value distribution. Horizontal axis being the function (y) value, vertical axis is count. On the left is the function value of thee problematic input, right is for random input.

Code

The parameters of the polynomial and the problematic inputs can be found here: https://drive.google.com/drive/folders/14xqPK7M8msCJpdJ6qsHuLggNt90gcPjC

1. Original function that I sampled from. Input is 32 dimensions

import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression

# 4th degree polynomial features
poly = PolynomialFeatures(4)

# regression parameters stored in json file
reg = LinearRegression()
with open('regression.txt', 'r') as file:
    reg_params = json.load(file)
reg.coef_ = np.array(reg_params['coef_'])
reg.intercept_ = reg_params['intercept_']
reg.rank_ = reg_params['rank_']
reg.singular_ = np.array(reg_params['singular_'])

def source_function(X):
    try:
        X = poly.transform(X)
        return reg.predict(X)
    except ValueError:
        X = poly.transform(X.reshape(1,-1))
        return reg.predict(X)[0]

2. Neural network

import torch
import torch.nn as nn
import torch.optim as optim
import torch.utils.data as Data
from torch.nn import Linear, ReLU

# MLP class
class mlp(nn.Module):
  def __init__(self, **kwargs):
    super().__init__()
    self.layer1 = nn.Linear(in_features=kwargs["input_shape"], out_features=48)
    self.layer2 = nn.Linear(in_features=48, out_features=48)
    self.layer3 = nn.Linear(in_features=48, out_features=48)
    self.layer4 = nn.Linear(in_features=48, out_features=48)
    self.pred = nn.Linear(in_features=48, out_features=1)
  
  def forward(self, features):
    x = self.layer1(features)
    x = torch.relu(x)
    x = self.layer2(x)
    x = torch.relu(x)
    x = self.layer3(x)
    x = torch.relu(x)
    x = self.layer4(x)
    x = torch.relu(x)
    prediction = self.pred(x)
    return prediction

3. Sampled data

# load up datapoints, this is the problematic dataset
# input domain is limited to [-1, 1] for all dimensions

X_train = np.genfromtxt('X_train.csv', delimiter=',')
# get corresponding y values by feeding X_train to defined function
y_train = source_function(X_train)

# a randomly generated dataset
X_train_random = scipy.sparse.random(10000, 32, density=0.25).A
X_train_random  = X_train_random *2-1 # inputs to be within [-1, 1]
y_train_random = source_function(X_train_random)

4. Training code

train_dataset = Data.TensorDataset(torch.from_numpy(X_train).type(torch.DoubleTensor),
                                   torch.from_numpy(y_train).type(torch.DoubleTensor))

train_loader = Data.DataLoader(dataset=train_dataset, batch_size=32, 
                               shuffle=True, num_workers=2,)

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

model = mlp(input_shape=dim).to(device)
model = model.double()

optimizer = optim.Adam(model.parameters(), lr=5e-3)

criterion = nn.MSELoss()

# Training loop

epochs = 500
for epoch in range(epochs):
    loss = 0
    for batch_features, out in train_loader:
        batch_features = batch_features.to(device)
        
        optimizer.zero_grad()
        
        outputs = model(batch_features.double())
        
        train_loss = criterion(outputs, out)
        train_loss.backward()
        
        optimizer.step()

        loss += train_loss.item()
    
    # compute the epoch training loss
    loss = loss / len(train_loader)
    
    # display the epoch training loss
    print("epoch : {}/{}, loss = {:.6f}".format(epoch + 1, epochs, loss))

Hardware: Google Colab non-GPU

Any help would be greatly appreciated!