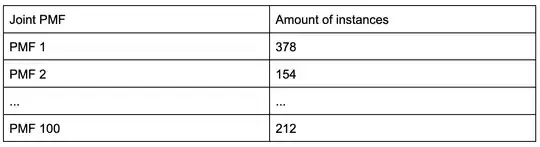
I have 100 unique joint probability mass functions with a dataset noting the prevalence of instances from each joint pmf, like this:
The total amount of instances in this case would be 16,073. Each joint PMF looks something like this:
{'F': 0.3, 'M': 0.7},
{'0–18': 0.1,
'19–25': 0.3,
'26–35': 0.2,
...
},
{'African American': 0.13,
'Asian': 0.2,
'Caucasian': 0.6,
...
}, ...
Each joint PMF can be assumed independent (i.e. the probability of an instance is the product of the marginal distributions).
I have utilized stratified sampling to represent each joint PMF based on the number of instances in the dataset. For example, for a random sample of n=100k, there are approximately 100k/(16.073k) * 378 = 2,352 instances from PMF 1, 959 instances from PMF 2, ... , 1,319 instances from PMF 100. Resulting in a dataset (with 100k rows) like this:
I'm trying to calculate the Jensen–Shannon distance between two datasets that look like the first embedded table with a different number of instances (but the same 100 unique PMFs). Since there is no closed form solution for JS-distance for joint PMFs, I'm trying to implement a monte carlo simulation approximation via this.
However, I'm stuck on how to do this since my dataset has multiple joint pmfs instead of a single joint pmf. Any ideas would be very helpful! Thank you so much!