I have successfully generated samples from the 1D Epanechnikov kernel, following the routine described on page 236 in "Nonparametric Density Estimation" by Devroye and Gyorfi (Also described in this stats post), where
- Generate three independent uniform samples [-1,-1] $V_1, V_2, V_3$.
- If $|V_3| > |V_1|$ and $|V_3| >| V_2|$, then return $W=V_2$ else return $W=V_3$
Results in the following samples:
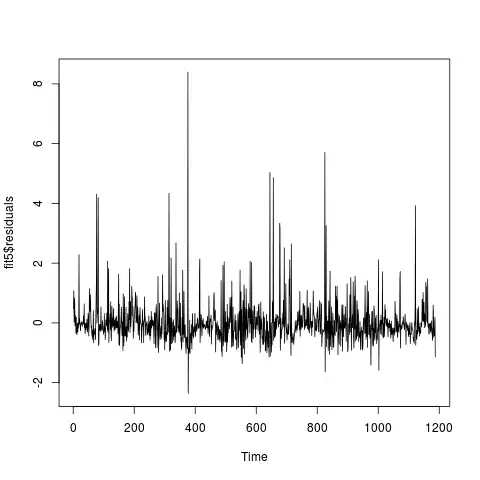
I naively assumed that in order to sample in high dimensions, one could simply sum two independent samples from the kernel, however that results in the following
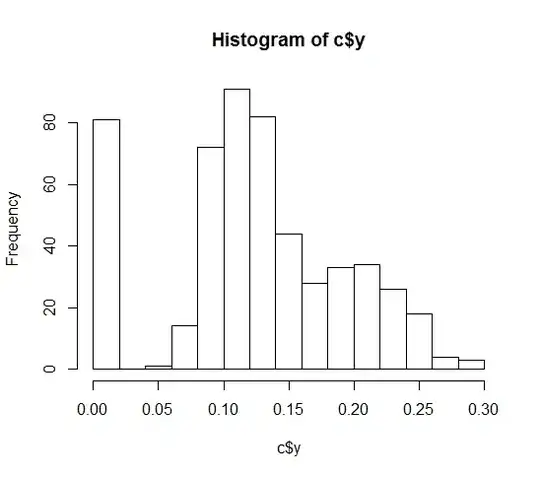
The outer ring shows the $||H||_2$ radius (with H the bandwidth matrix). Page 236-237 in "Nonparametric Density Estimation" by Devroye and Gyorfi also discusses the requirements of the higher dimensional kernel. I'm however unsure how to sample these higher dimensions. Can the above algorithm be extended to n-dimensions?