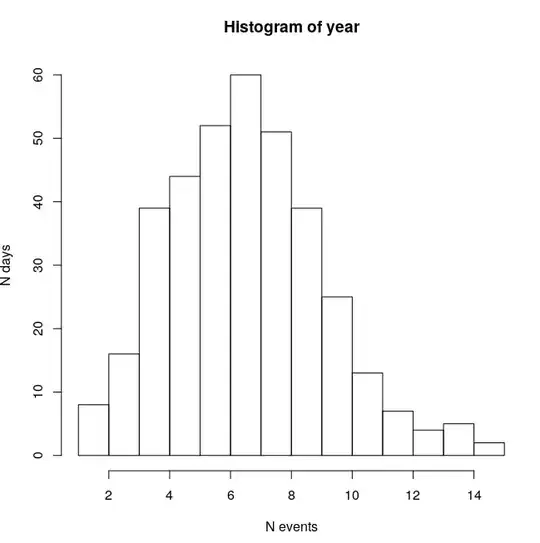
I am trying to distribute a given (fixed) number of events of a year over the respective year. The empirical distribution can be modelled with a Poisson distribution because there are usually only between 1 and 14 events per day. I tried looping through the days of the year and generating a random number of events from a poisson distribution. The point at which I struggle is to distribute ALL events. If I overestimate the distribution, there are no events at all at the last weeks of the year and if I underestimate the distribution, there are several events left but they all need to take place in the considered year. Is there any way to distribute all events?
Thanks a lot for your help and inspirations!