This is all to settle a methodology debate and neither of us have a good enough grasp of the subject to come to a satisfying solution.
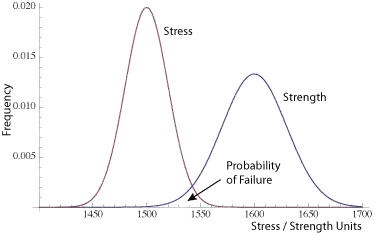
We have this Stress-Strength model of a failure :
Bascially, the strength of a component (the fuselage of an airplane for example) is defined by a normal distribution (because no two parts are exactly the same) and the stress is defined by by a normal distribution as well (it represents all possible stresses that the component can experience during its life cycle).
The probability of failure is defined by the region in which the stress is higher than the strength.
$P(Strength < Stress) = \Phi(-\frac{\mu_{Strength} - \mu_{Stress} }{\sqrt{\sigma^2_{Strength} + \sigma^2_{Stress}}}) $
So given that we want to estimate two things :
- What is the probability of failure of two components ? We can argue that the strength distribution already kinda represents the fact that it's not a unique component but then it doesn't feel right as using more components does not change the probability at all.
- What is the failure rate (in probability/hour) of the component assuming it's life cycle is T hours long ? The naive approach we've seen used simple divides the probabilty by T, and it doesn't feel right either as you could arbitrarily define a new life cycle which is exactly the same as two times the original back to back and then divide the probability by 2T at no cost.