1

I have a simple model.

y ~ x

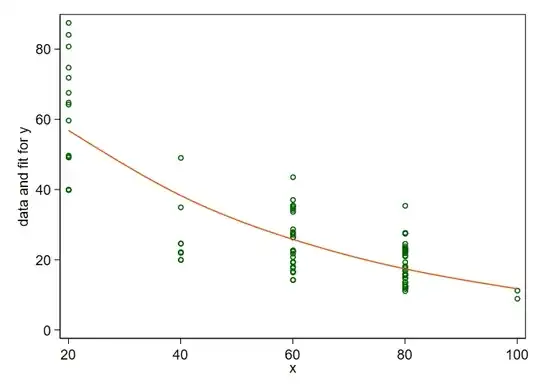
y is continuous (habitat gained per million $)

x is continuous (percent completeness of database used to generate y)

However, the residuals aren't normal.

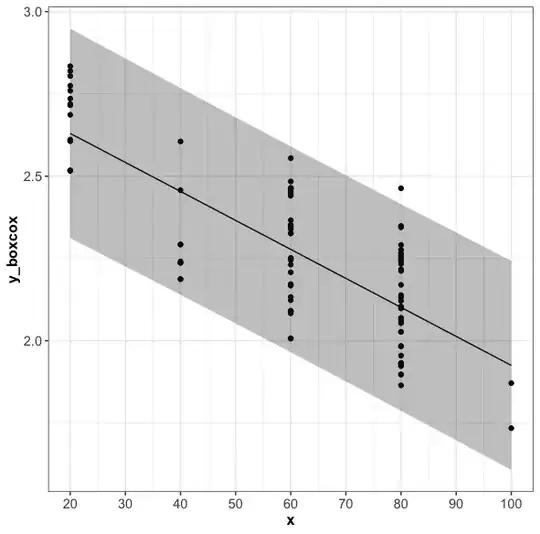
Using the lowest absolute AIC I have determined that the best transformation for my dependent variable comes from using Box-Cox. Lambda = -0.22.

How would I report the results after putting this through a Pearson's Correlation and linear model in R?

Transformed - surely meaningless to the reader.

Or

Back-transformed - if so how?

i.e.

Transformed

Increasing x significantly decreased y (where y is transformed using a Box-Cox transformation where lambda = -0.14, r(968) = -0.76, 95% Ci [-0.78 -0.72], p = <0.001, intercept = 3.23, slope = -0.011)

Back-transformed

Increasing x significantly decreased y (where y is back-transformed from a Box-Cox transformation where lambda = -0.14, r(968) = -0.76, 95% Ci [1.86 2.21], p = <0.001, intercept = 75.01, slope = 0.99)

Data

dput(cv_dat)
structure(list(x = c(60, 80, 80, 80, 80, 80, 60, 40, 80, 40, 
60, 60, 80, 80, 20, 80, 60, 60, 80, 80, 80, 80, 40, 60, 80, 20, 
80, 80, 80, 20, 80, 20, 60, 40, 60, 40, 80, 60, 80, 20, 80, 80, 
20, 80, 40, 80, 60, 20, 20, 100, 60, 80, 60, 80, 80, 80, 80, 
60, 20, 60, 60, 60, 60, 60, 20, 60, 20, 60, 60, 80, 40, 80, 100, 
60, 60, 80, 80, 20, 20, 20, 80, 40, 80, 80, 60, 60, 40, 40, 100, 
80, 80, 20, 40, 80, 60, 80, 60, 80, 20, 40), y = c(34.7147333333333, 
22.2961111111111, 20.9838761904762, 13.6910047619048, 23.83764, 
12.3437625, 26.4331555555556, NA, 27.4610266666667, 24.6421583333333, 
16.6102944444444, 26.4134, 22.8710666666667, 21.1918380952381, 
49.4057666666667, 23.3209333333333, 34.2554666666667, 35.2223555555556, 
22.4638666666667, 15.8720333333333, 11.7405725490196, NA, NA, 
14.2798428571429, 13.6565571428571, NA, 17.0589133333333, 11.7647058823529, 
23.1394444444444, 84.1246, 12.5, 71.8905666666667, 21.8039416666667, 
20, 14.2517523809524, 49.0612888888889, NA, 28.73436, 12.4514833333333, 
49.7169333333333, 11.1078740740741, 16.8650545454545, 67.6015666666667, 
14.7961179487179, 20, 27.6441166666667, 33.6938666666667, 39.88104, 
87.5281333333333, NA, 27.5380444444444, 19.3335833333333, 37.0873777777778, 
21.8931333333333, 17.6113733333333, 17.9914533333333, 27.6807333333333, 
22.4254333333333, 59.7117111111111, 19.4141066666667, 27.9112111111111, 
16.6534333333333, 18.0147090909091, 16.4096555555556, 80.8001333333333, 
27.1562444444444, 64.2548666666667, 19.2395933333333, 22.64985, 
12.9968488888889, 22.2222222222222, 22.8283444444444, 8.93967575757576, 
35.4892, 17.6795575757576, 35.4194666666667, 18.2141111111111, 
40, 74.7947, 40, 12.2866375, 22.036637037037, 15.5196944444444, 
15.7524333333333, 43.5638666666667, 22.704825, NA, 22.0478444444444, 
11.236775, 14.7893846153846, NA, 64.8276, 24.675475, 15.9975151515152, 
35.4629333333333, 12.4224458333333, 20.8199555555556, 24.5840666666667, 
49.1685333333333, 34.9769333333333)), row.names = c(NA, -100L
), class = c("tbl_df", "tbl", "data.frame"))

Code

library(MASS)
library(dplyr)
library(bimixt)
library(broom)
library(ggplot)

cv_dat <- dat2 %>% 
  rename(x = percent, y = roi) %>%
  sample_n(100) %>% 
  dput()

dput(cv_dat)

plot(y ~ x, cv_dat)

bc <- MASS::boxcox(y ~ x,
                   data = cv_dat)
(lambda <- bc$x[which.max(bc$y)])

model_bc <- lm(((y^lambda-1)/lambda) ~ x, cv_dat)


# intercept and slope
model_bc$coefficients
# Back-transformed intercept and slope
boxcox.inv(model_bc$coefficients, lambda)

# pearson's
res <- cor.test(cv_dat$x, (cv_dat$y^lambda-1)/lambda, 
                method = "pearson")

# 95% confidence intervals
res$conf.int
# Back-transformed 95% confidence intervals
boxcox.inv(res$conf.int, lambda)

cv_dat_aug <- augment(model_bc, newdata = cv_dat, interval = "prediction") %>%
  mutate(.fitted_trans = boxcox.inv(.fitted, lambda),
         .lower_trans = boxcox.inv(.lower, lambda),
         .upper_trans = boxcox.inv(.upper, lambda))

ggplot(cv_dat_aug, mapping = aes(x = x, y = (y^lambda-1)/lambda)) +
  geom_point() +
  geom_line(mapping = aes(y = .fitted)) + 
  geom_ribbon(aes(ymin = .lower, ymax = .upper), col = NA, alpha = 0.3) + 
  scale_x_continuous(breaks = seq(10, 100, by = 10)) + 
  ylab("y_boxcox") + 
  xlab("x")

Box-Cox transformed y and fitted line

Box-Cox transformed y as a function of x

user3725599
  • 13
  • 3
  • I suggest you show some data. Tukey's ladder of powers includes reciprocal square root (power $-0.5$); the approach of estimating a power more finely is more in the spirit of Box-Cox. What could be meaningful to the reader is to show a graph of the data and your fitted curve. – Nick Cox Sep 07 '21 at 10:09
  • OK say I used Box-Cox to estimate the transformation. Are you suggesting I show a graph of the transformed data with the fitted curve? – user3725599 Sep 07 '21 at 10:27
  • No. I am suggesting you (1) list the data, or a sample (2) show a plot of the data with the fitted curve. If I understand correctly you can also tell us the intercept and gradient of your fit. – Nick Cox Sep 07 '21 at 10:44
  • Thanks for posting the data. Interim report. I wouldn't transform at all. I suggest Poisson regression with robust standard errors. More later. – Nick Cox Sep 07 '21 at 12:58
  • Thanks. It's poisson even though y is continuous and x = percent and could be any value between 0 and 100 (therefore continuous?), neither being count data? – user3725599 Sep 07 '21 at 13:42
  • The predictor being continuous is neither here nor there. The outcome being continuous is not important either. You could experiment with other error families to explore the point. – Nick Cox Sep 07 '21 at 15:21
  • What is the optimal lambda value in your box-cox transformation? This might help us provide hints for an alternative and interpretable transformation. – Robert Bassett Sep 07 '21 at 15:34
  • For this sample data the optimal box-cox lambda = -0.22 – user3725599 Sep 07 '21 at 15:46
  • The estimated lambda was earlier reported as lower. Regardless, $-0.22$ would be treated by many analysts (me any way) as indicating logarithm in practice, and so consistent with use of a log link if the approach is to use a generalized linear model rather than to transform the response. – Nick Cox Sep 07 '21 at 16:44
  • 1
    The optimal Box-Cox power must be close to $0,$ not $-0.22.$ The plot clearly shows $-0.22$ is too strong: the vertical spreads increase from top to bottom. This further justifies @NickCox's logarithm suggestion. The methods explained at https://stats.stackexchange.com/a/35717/919 suggest (1) regressing $\log(y)$ against $\log(x)$ and (2) treating the two values with $x=100$ as outliers. BTW, what is the reason for the missing values? That could influence the analysis. – whuber Sep 07 '21 at 17:53
  • 1
    Box-Cox is often used in ways that its original authors would not obviously endorse. One of their original examples in their 1964 paper is loosely similar: an estimated power near 0 is used to suggest logarithmic transformation, which on other grounds seems natural to the problem. The title of this thread doesn't seem to indicate its main thrust, which I take to be that a particular transformation is "surely meaningless to the reader". We can't guess who your readers will be, or how well informed they are, but my question offers a direct approach to the analysis of the data. – Nick Cox Sep 07 '21 at 20:04
  • 1
    The first version of this question indicated a power choice of $-0.4$; it's now stated to be $-0.22$. I ran a Box-Cox analysis in Stata which loosely agrees on a power of about $-0.2$ but more crucially gives a confidence interval that includes $0$. @whuber's suggestion of logging $x$ and treating points at $x = 100$ as outluers is on other grounds. – Nick Cox Sep 07 '21 at 20:06
  • Full dataset (n = 970) has a box-cox lambda of -0.14. Missing values can be ignored. In the full data there are 26 values for x = 100 compared to 380 values for x = 80, so the data is biased towards x = 20, 60, 80 rather than x = 100 is an outlier. – user3725599 Sep 08 '21 at 09:29
  • I am not minded to suggest that x = 100 points are outliers. My analysis with the subset supplied does not imply that they are out of line with the general relationship. – Nick Cox Sep 08 '21 at 11:01
  • 1
    Just providing clarity – user3725599 Sep 08 '21 at 11:13

1 Answers1

2

enter image description here

Poisson regression is just (in this case and others) a traditional name for what in essence is fitting $\exp(Xb)$ as functional form, specifically for one predictor -- generically and in this particular case called $x$ -- $y_0 \exp(bx)$, where $b$ will turn out to be negative for these data. So, it's a generalized linear model with log link; the precise assumptions about error structure are secondary, although Poisson error coupled with robust standard errors should work about as well as any, as from the graph there is a fairly strong indication of heteroscedasticity. See e.g. this blog post for one version of the story. The response being continuous not discrete is immaterial.

The question does not explain whether the response or outcome $y$ is necessarily always positive or always non-negative, but if that is so then the functional form respects that insofar as the mean response is always positive. (That is, can habitat gained be negative, because it is habitat lost?)

Independent checks with generalized linear models with power link $-0.4$ give very similar predictions. It's partly a matter of taste and of experience but I would go for Poisson regression as a direct approach. (That's not quite what the OP did, which was to transform the response and follow with plain regression.)

I used Stata for the fitting and plotting.

. poisson y  x, vce(robust)
note: you are responsible for interpretation of noncount dep. variable.

Iteration 0:   log pseudolikelihood = -362.35156  
Iteration 1:   log pseudolikelihood = -362.34892  
Iteration 2:   log pseudolikelihood = -362.34892  

Poisson regression                                      Number of obs =     92
                                                        Wald chi2(1)  = 175.03
                                                        Prob > chi2   = 0.0000
Log pseudolikelihood = -362.34892                       Pseudo R2     = 0.4439

------------------------------------------------------------------------------
             |               Robust
           y | Coefficient  std. err.      z    P>|z|     [95% conf. interval]
-------------+----------------------------------------------------------------
           x |  -.0197382   .0014919   -13.23   0.000    -.0226624   -.0168141
       _cons |   4.435126   .0945831    46.89   0.000     4.249746    4.620505
------------------------------------------------------------------------------
Nick Cox
  • 48,377
  • 8
  • 110
  • 156