Bernoulli and Binomial logistic regression's likelihood in practise

Question

I'm calculating Logistic Regression for a purticular dataset and kind of lost while estimating parameters with likelihood function. I stuck when I tried to match my dataset to the formulas below. I found 2 versions of likelihood function - when $y_i$ is Binomial and $y_i$ is Bernoulli distributed.

\begin{equation} L(\beta|y)={\displaystyle \prod_{i=1}^{N} \frac{n_i!} {y_i!(n_i-y_i)!}} \pi_{i}^{y_i}(1-\pi_i)^{n_i - y_i} \tag 1 \end{equation}

and

\begin{equation} L(\beta_0,\beta_1)= \displaystyle \prod_{i=1}^{N}p(x_i)^{y_i}(1-p(x_i))^{1-y_i} \tag 2 \end{equation}

Sources:

1. First: https://czep.net/stat/mlelr.pdf (page 3 equ. 2)
2. Second: http://www.stat.cmu.edu/~cshalizi/uADA/12/lectures/ch12.pdf (page 5 equ. 12.6)

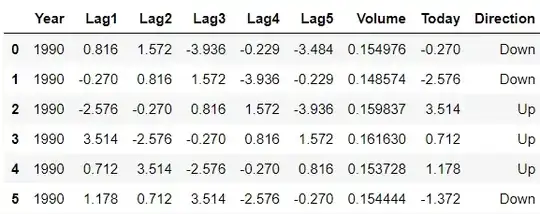
I'm using dataset from An Introduction To Statistical Learning, by Hastie. Weekly dataset.
https://www.statlearning.com/resources-first-edition

I want to get understanding of what is what in the formulas matching every member of formulas to some piece of information from the dataset.

1. Binomial case:
   $ N = 6 $ - is number of observarions(I thought it should be equal to number of rows but there is $n_i$);
   $ n_i = 6 $ - number of rows;
   $ y_i = 3 $ - number of successes/Up's in my dataset;
   $ \pi_i = \frac{1}{1+exp(-(\sum_{k=0}^K x_{ik}\beta_k))} $ - probability of 1 success/Direction Up;
   $ \pi_i - 1 $ - probability of 1 failure/Direction Down;
   We have $ \pi_i^3 $ because we have three rows with success case;
   We have $ (\pi_i-1)^{(6-3)} $ because we have three rows with failure case;
   $ \frac{n_i!}{y_i!(n_i-y_i)} $ - this is number of combinations to get 3 successes with 6 trials.
   
   My questions here:
   A. Could you please explain why is $\prod_{i=1}^{N}$ used here and when it is usefull? Or what is the example of dataset when we need to find a products of the product $\frac{n_i!} {y_i!(n_i-y_i)!} \pi_{i}^{y_i}(1-\pi_i)^{n_i - y_i}$
   B. What is gonna be N in scope of my dataset?\

Updated 2. Bernoulli case:
As far as I undertand $N $ - is number of rows in my dataset. So that formula can be expanded like $$L(\beta_0,\beta_1)= \displaystyle \prod_{i=1}^{6}p(x_i)^{y_i}(1-p(x_i))^{1-y_i} = $$ $$p(x_0)^{0}(1-p(x_0))^{1} * p(x_1)^{0}(1-p(x_1))^{1} * p(x_2)^{1}(1-p(x_2))^{0} * p(x_3)^{1}(1-p(x_3))^{0} * p(x_4)^{1}(1-p(x_4))^{0} * p(x_5)^{0}(1-p(x_5))^{1} = $$ $$p(x_i)^{3}(1-p(x_i))^{3} $$ assuming that $x_0=x_1=...=x_i$

Is this right way to calculate that formula for Weekly dataset?

Answer 1

A. Could you please explain why is $\prod_{i=1}^{N}$ used here and when it is usefull? Or what is the example of dataset when we need to find a products of the product $\frac{n_i!} {y_i!(n_i-y_i)!}\pi_{i}^{y_i}(1-\pi_i)^{n_i - y_i}$

You would use this likelihood formulation when you have observations from multiple Binomial random variables, where the $i$th Binomial random variable has $n_i$ trials and presumed probability of success equal to $\pi_i$. In this case, the maximum likelihood estimate of each $\pi_i$ would be $y_i/n_i$, e.g. $\hat\pi_1 = y_1/n_1$, $\hat\pi_2 = y_2/n_2$, etc.

B. What is gonna be N in scope of my dataset?

If you are assuming that there is a common probability of success in each row of your data, then $N=1$ and $n_1=6$ for your situation. If you are allowing that there may be a different probability of success in each row of your data, then $N=6$ and $n_1=n_2=\ldots=n_6=1$.

As far as I undertand $N $ - is number of rows in my dataset. So that formula can be expanded like $$L(\beta_0,\beta_1)= \displaystyle > \prod_{i=1}^{6}p(x_i)^{y_i}(1-p(x_i))^{1-y_i} = $$ $$p(x_i)^{0}(1-p(x_i))^{1} * p(x_i)^{0}(1-p(x_i))^{1} * > p(x_i)^{1}(1-p(x_i))^{0} * p(x_i)^{1}(1-p(x_i))^{0} * > p(x_i)^{1}(1-p(x_i))^{0} * p(x_i)^{0}(1-p(x_i))^{1} = $$ $$p(x_i)^{3}(1-p(x_i))^{3}$$

Is this right way to calculate that formula for Weekly dataset?

No, what you have written is not correct unless $x_i$ is constant for each $i$, that is, unless $x_i\equiv x$.