I have a data set that has as DV the preference of spatial reproduced audio files (OLE) and as IVs the preference of only their content and the sensation of envelopment. All the variables are continuous. The aim is to predict OLE based on the 2 dependent variables.
I fit a linear regression model (all assumptions are met) and I got R2=0.631 (both DVs are statistically significant).
However, I observed that when my DV is lower than 0.55 (all variables are normalized, so a value of 0.5 corresponds to a neutral state) the model overestimates, while when DV is greater than 0.55 it underestimates (See the Graph)
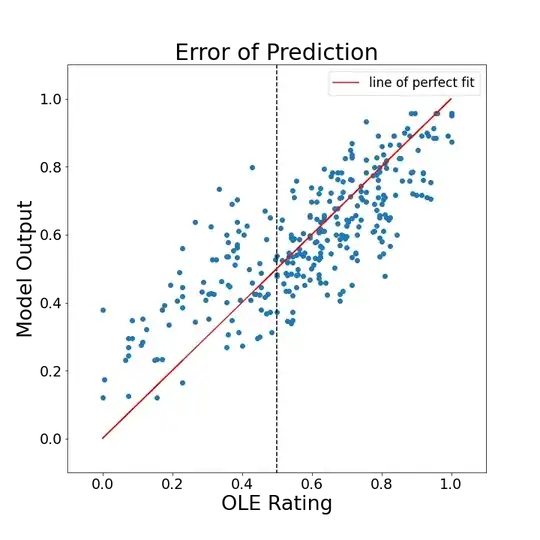
So a first thought is that the 2 dependent variables may have different weights in each subpart of the DV (one for values of OLE less than 0.55 and one for values greater than 0.55).
I created a dummy variable HighOle which gets values 1 if the DV is greater than 0.55 and zero if it is less and I multiplied this dummy with both my IVs, in order to see the impact of each variable in each subpart of the data. In the model of course I included and the original variables, so I got:
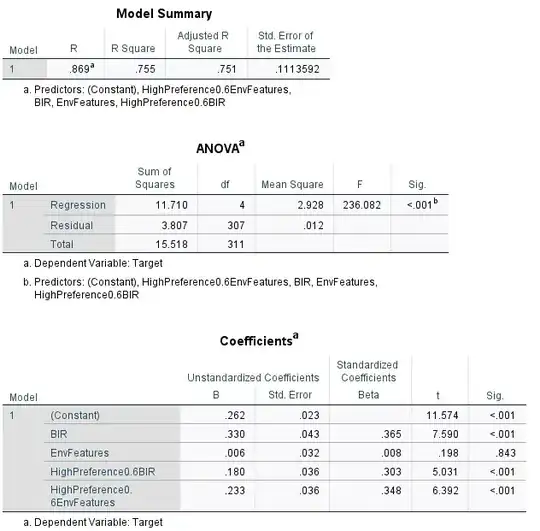
EnvFeatures: sensation of envelopment BIR: the preference of the content
I don't want to create a generalizable model which will predict new data, but to get an interpretation of the way people assess their preference on spatial audio systems and which factors take under consideration when they like or dislike something.
The question is if this methodology is correct because I can't find something similar on the Internet (it is like a piecewise linear regression with the only difference being that the segmentation is done in the dependent variable).