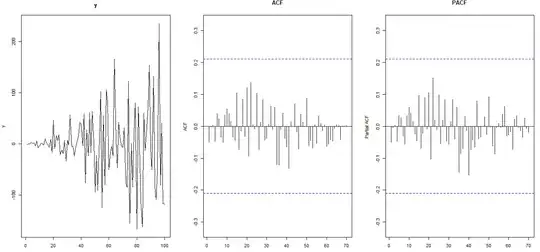
The code below generates series y, which by design is clearly non-stationary. The ADF test below was run with 12 lags to yield (what visually appear to be) uncorrelated residuals and it would have us conclude that y is stationary. What went wrong here?
set.seed(100)
y<-rep(NA,100)
for (i in 1:100) {
y[i]<-rnorm(1,mean=0,sd=i)
}
par(mfrow=c(1,3))
plot(y,type="l",main="y")
u<-urca::ur.df(y=y, type = "none",lags=12)
summary(u)
forecast::Acf(u@res,lag.max=70,type="correlation",main="ACF",xlab="")
forecast::Acf(u@res,lag.max=70,type="partial",main="PACF",xlab="")