2

I have a regression problem in which the outcome variable is a proportion with values in the interval $[0, 1]$. My question is related to this one which is about how to model an outcome variable with values $[0, 1]$. My question is different because I am asking what could be done to address the values that are undefined in the logistic function.

My outcome variable would need to be pre-transformed before the logistic transformation since the logistic transformation $\log(\frac{y }{1 − y})$ is undefined at $y = 1$, and about half of its values are equal to $1$. How would you recommend I overcome $y = 1$ being undefined in the logistic transformation function?

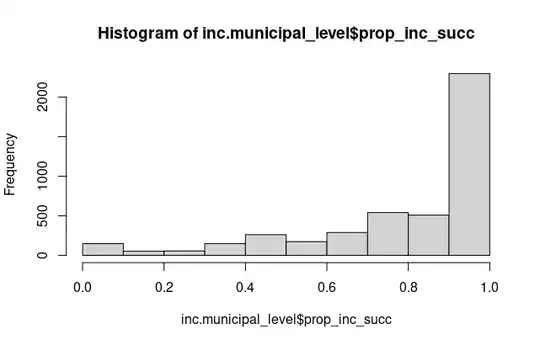
About half of the are values equal to 1, and this is the distribution: Distribution of outcome variable

Nick Cox
  • 48,377
  • 8
  • 110
  • 156
Reed Merrill
  • 21
  • 5
  • 5
    In almost all such cases, the solution is to use logistic regression (or some other suitable generalized linear model) instead of trying to transform the response. Is there a reason you are committed to using a transformation? – whuber Aug 21 '21 at 19:22
  • @whuber, Good to know. I'm exploring alternative modeling approaches to demonstrate robustness. I'll also do a logistic regression thanks to your suggestion – Reed Merrill Aug 21 '21 at 19:32
  • 1
    Another possibility is beta regression,search this site. Otherwise, maybe one of this answers your Q: https://stats.stackexchange.com/questions/216122/what-is-the-difference-between-logistic-regression-and-fractional-response-regre, https://stats.stackexchange.com/questions/225027/how-can-standard-logistic-regression-model-fractional-response-variable-while-de, https://stats.stackexchange.com/questions/530149/help-with-needed-with-fractional-outcomes-logit-regression/530227#530227 – kjetil b halvorsen Aug 22 '21 at 15:30

0 Answers0