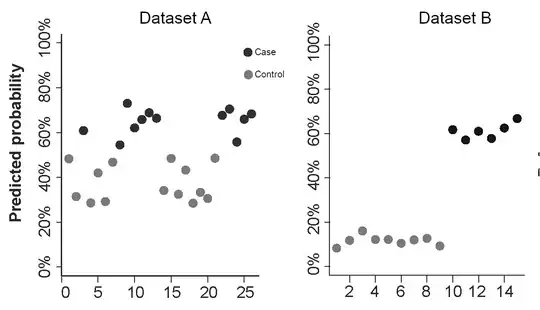
I used 3 continuous predictors (standardized to unit scale with mean = 0) in a glm model to solve for a two-class categorical problem (case, control). The model was selected in a previous published work, we just repeated the predictors measurements in the two new datasets below.
How can I explain the discrepancies between the predicted probabilities across these two datasets?
I was told that the first one is poor because it is close to 50% probability (i.e., random), even though it correctly classifies all samples. I'm not sure if we can make that claim by using the model's predictive proabibility...
Accuracy and 95% CI for:
- dataset A: 100% (86.7 % - 100%)
- dataset B: 100% (78.19% - 100%)
Any input is appreciated.