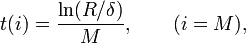In page 164 of the book “Probability theory: the logic of science” the author says that:
$$ p(D|\theta I) = \prod_{i=1}^{n} p(x_i|\theta I) = \theta^r(1-\theta)^{n-r} $$
$ \theta $, in this equation, represents the proposition:
$$ \theta = p(x_i = 1 | I), \forall i $$
How is $ p(x_i = 1|\theta I) $ equal to $ \theta $ when it is clearly not the same as $ p(x_i = 1 | I) $?
Edit:
This thread helped me a lot - How is data generated in the Bayesian framework and what is the nature on the parameter that generates the data?