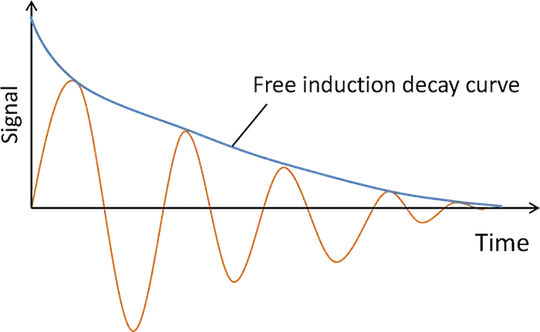
Here are the 3 steps I used to extract parameters from an FID. Note that this is only what I could come up with in a short amount of time, so others may have better solutions.
Notes:
- Every once in a while, SciPy seems to fall in a "false minimum" problem, where it believes it has found the curve of best fit, but really hasn't. I'm not sure why this happens or how to fix it.
- Yes, I am extracting only a finite amount of points from the FID, in this case from the domain (-9,10). Of course, this can be expanded.
Step 1: Create a Random Damped Oscillator
A damped oscillator is analogous to an FID. The inputs = [], outputs = [] arrays serve to store discrete values from the graph. These arrays will later be converted into a pandas pd.DataFrame, which will be the input for the regression network. Use numpy.rand() to generate random values for A, w, T2. Then use a for loop to add values to the inputs = [], outputs = [] arrays.
inputs = [], outputs = []
y = A*np.cos(w*dom)*(2.718**(-dom/T2))
def expDec(t, A, w, T2):
return A*np.cos(w*t)*(2.718**(-t/T2))
for i in range(-9, 10):
inputs.append(i)
outputs.append(expDec(i, A, w, T2))
Step 2: Create DataFrame
Create a pandas pd.DataFrame. This seemed the best way to "hand-over" the graph's values.
points = {'Input': inputs, 'Output': outputs}
x = pd.DataFrame(points, columns = ['Input', 'Output'])
Step 3: Best-Fit Curve
There's a few parts to this. First, explicitly inform the program what type of graph you want to be extracting the parameters from. In our case, it's an FID, analogous to a Damped Oscillator. Then, retreive the values from the graph and store them in the ins, outs variables. Pass these variables onto SciPy's curve_fit function. This function will return what SciPy believes are the best parameters that fit the FID. Now pass on these parameters to realFunc(), which will append all the output values in the domain (-9,10) to the fit=[] array.
def realFunc(t, A, w, T2):
return A*np.cos(w*t)*(2.718**(-t/T2))
ins = x['Input'].values
outs = x['Output'].values
fit = []
constants = curve_fit(realFunc, ins, outs, maxfev=1000)
for i in range(-9,10):
fit.append(realFunc(i, A_fit, w_fit, T2_fit))
plt.plot(x['Input'], x['Output'])
plt.plot(x['Input'], fit,"ro-")
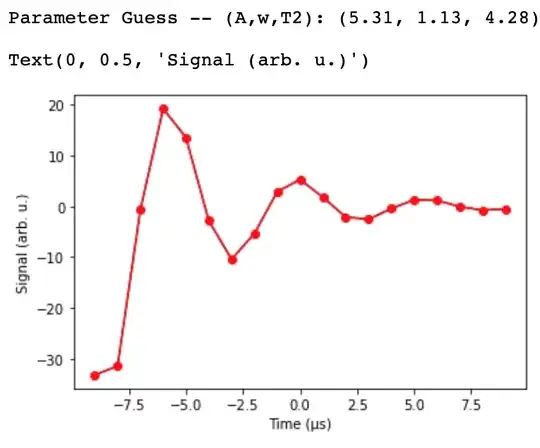
And that's it! All of these steps can be followed at the Interactive Jupyter Notebook found here.