How to calculate Quasi-Monte Carlo integration error when sampling with Sobol's sequence?

Question

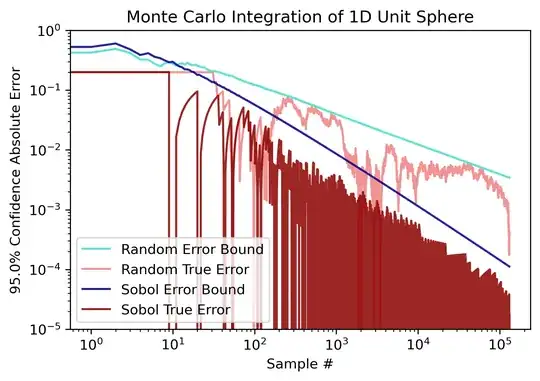
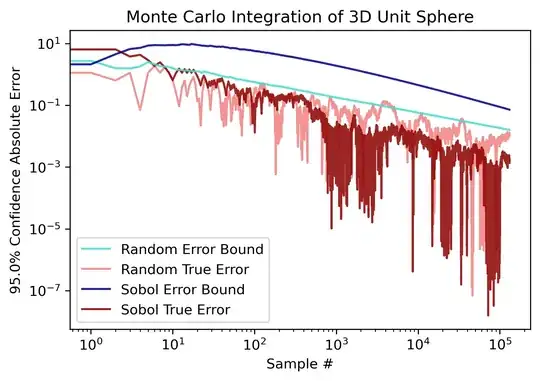
My understanding is that QMC integration using random sampling will converge with $O(\frac{1}{\sqrt{n}})$, while using Sobol's sampling will converge with $O(\frac{(\log{n})^d}{n})$. However I'm having trouble converting this big O notation into concrete error bounds.

This source gives an equation for calculating error bounds when random sampling. Given a set of random samples with variance $\sigma^2$ drawn from volume $V$ and a chosen confidence level $\gamma \in (0,1)$, we can find the bounding integration error from $\epsilon_\gamma = V\sigma\Phi^{-1}(\gamma)\frac{1}{\sqrt{n}}$, which follows from the central limit theorem.

Is finding the error bounds when Sobol sampling just as easy? Should I be using this? $\epsilon_\gamma = V\sigma\Phi^{-1}(\gamma)\frac{(\log{n})^d}{n}$

In my empirical tests of 1-dimensional sequences it seems to be a reasonable (if anything, too high) upper bound, but I want to make sure I'm theoretically grounded here since higher dimensions are harder to test.

Answer 1

You might find the paper Quasi-random sequences and their discrepancies by Morokoff and Caflisch (1994) useful.

https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.298.5482&rep=rep1&type=pdf

They give bounds of the form $$ \left|\int_{[0,1]^d}f(x)dx - \frac{1}{N}\sum_{i=1}^N f(x_i) \right| \le V(f) D_N^* \, , $$ where $V(f)$ is the variation of $f$ in the sense of Hardy and Krause and $D_N^*$ is the star-discrepancy with $$ D_N^* = \mathcal{O}\left( \frac{(\log N)^d}{N} \right) \, . $$ The paper also provides some guidance on the missing pre-factor. In general these bounds are only useful if the number of points is very large. Moreover, the variation $V(f)$ may be quite complicated and intractable to compute.

I don't know how well this would work, but a simple solution that might be worth trying is resampling your points to compute bootstrap-type estimates of the confidence intervals.

Answer 2

Thank you @TAlsup for that reference, it really helped clarify the situation. Here's a summary of what I learned:

• Unfortunately, the theoretical error bounds for low-discrepancy sequences are only useful for large N at low dimensions. Once you pass 2-3 dimensions, the N necessary to lower the error bounds becomes intractably large. (See first 3 plots)

• This behavior is somewhat physical - sobol convergence starts closer to $O(\frac{1}{\sqrt{n}})$ and only approaches $O(\frac{(\log{n})^d}{n})$ at large $n$. However, as $d$ increases, the inflection point increases super-exponentially. In other words, at higher dimensions sobol sampling does not provide much of a benefit over random sampling for integration.

• Calculating actual discrepancy of the sample points with the scipy.stats.qmc.discrepancy() function is too slow for normal use, and $V(f)$ depends on the specific Sobol digital net value of $t$, which is specific to the implementation and varies among different dimension pairs (see Joe & Kuo, 2008). Faure & Lemieux (2010) says the situation hasn't really gotten better since the Morokoff & Caflisch (1994) paper.

• They have a better way to calculate the error bounds for random samples. The mean value of the expected error is given as $\epsilon_{0.5} = V\sqrt{\frac{2^{-d} - 3^{-d}}{n}}$. This next bit wasn't completely clear, but I think that the numerator can be thought of as the expected value of $\sigma$, so you can get the value at your confidence level as $\epsilon_{\gamma} = V\Phi^{-1}(\gamma)\sqrt{\frac{2^{-d} - 3^{-d}}{n}}$. In my empirical tests, this equation and the previous equation were dead on top of each other for low $d$, and once $d$ got bigger than about 7, this new equation provided much more realistic error bound. That lends me some confidence that I'm doing it right. (See last 2 plots)

What I've decided to do in practice is calculate both the random and sobol sampling error bounds, and for sobol sampling use the lower of the two. Sobol sampling will perform at least as well as random, so this is justified. My original bootleg coefficient for the sobol bounds seems reasonable, so I’m going to stick with it.