3

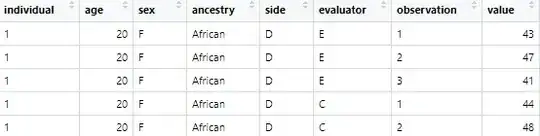
I hope you can steer me in the right direction. I'm helping a colleague analysing a dataset that consists of:

  • one dependent variable (value) measured 3 times (observation) by 3 people (evaluator) on the 2 sides (side - right/left) of an individual (~150 individuals)

  • several independent variables: one continuous (age), and 2 discrete (sex, ancestry).

  • the data also has NA has some evaluators skipped over a few individuals in one or more of the observation points.

    enter code here

His main questions concern the reproducibility of measurements and effect of independent variables:

  • for reproducibility I used intraclass correlation coefficients with relative success;
  • to look at the effect of independent variables, I would normally use some form of a linear model (ANOVA/ANCOVA).

However, I'm worried about the lack of independence between observations, basically the first assumption of a lot of these tests. I tried looking at mixed models (e.g. using 1 between subjects factor (sex) and 2 within subjects factors (evaluator & observation) ), but I couldn't find good examples of this application (particularly using R), and mixed models seem to focus on evaluating the impact of these within subject factors, when in fact I mostly just want to control for these and focus on the effect of the independent factors.

Questions: (1) Could I assume independence? (2) What would be an appropriate design model (@RobertLong 's correction)? (3 - slightly off topic) Any R pointers are welcome.

Update Following Robert Long's answer, I'm now working with a mixed model that looks like this lme(value ~ sex * side + age + ancestry + evaluator, data = L, random = ~1|individual, method = "ML", na.action = na.exclude) (using Andy Field's book)

However, now I have more questions: (1) How to follow up (especially considering that I want to understand the effect of sex while controlling for the effect of ´evaluator´. Would contrast be a good option? (2) Reading on this, I realised that lack of independence will also be an issue for the ICC I calculated. Could I calculate them from the mixed model? (Based on this: Computing repeatability of effects from an lmer model)

answer42
  • 105
  • 6
  • 1
    How many individuals do you have ? What is the "evaluator" variable (is that the 3 different people doing the measurements ?) Is it the same 3 people all the time, or are the more than 3 people (ie 3 different people for other individuals) ? – Robert Long Jul 07 '21 at 18:28
  • I edited the question to include the very pertinent info you requested. In summary: around 150 individuals; Yes; Yes. I appreciate any help. I'm used to the typical frequentist statistics but getting lost in a mixed model rabbit hole. Thank you. – answer42 Jul 07 '21 at 19:07

1 Answers1

5

(1) Could I assume independence?

No, because you have repeated measurements. Observations within one individual are more likely to be similar to other observations within the same individual than observations on other individuals. One way to handle this is to fit random intercepts for individuals in a mixed model. It also seems that evaluator is crossed with individual, but you don't have enough evaluators to justify fitting random intercepts for that, so you will need to fit fixed effects for evaluator.

(2) What would be an appropriate design?

Perhaps you mean model, not design ? The (study) design is the experiment itself which apparently has already been done. As for the model, a mixed model may be appropriate.

3 - (slightly off topic) Any R pointers are welcome.

I would start with a model such as:

value ~ age + sex + ancestry + side + evaluator + (1 | individual)

You could use the lmer function in the lme4 package for that.

Robert Long
  • 53,316
  • 10
  • 84
  • 148
  • Got it for question 1 and 2. Thank you. Re. R: (1) Should I ignore `observation`? Maybe `+observation*evaluator` or is this not appropriate? (2) is it okay to convert `factors` to `numeric`? To get a single p-value per variable (3) [trickier as you don't have my data] I get a surprising significant p-value for `side` (absent visually and when ignoring data structure) prob bc `sex` is unbalanced so could include `sex*size` (significant btw)? – answer42 Jul 07 '21 at 21:06
  • 1
    `observation` is the lowest level - there are no repeated measures within in it right ? if so then you don't need to include it. `observation*evaluator` if you expect an interaction between them, though based on the description I can't see why what would be. Factors to numeric: that usually doesn't make sense. With a binary variable it doesn't matter but if it's categorical with more than 2 levels then it does not make sense. As for p-values please ask a different question about, but p-values for mixed models are not well defined to begin with so please try not to be too concerned with them. – Robert Long Jul 07 '21 at 21:48
  • No repeated measures within `observation`; Factors to numeric: I was following Andy Field's book which suggests this as a way to evaluate effect of categorical variable overall rather than getting a different result for each factor level – answer42 Jul 08 '21 at 14:11
  • Please ask a seperate question about treating categorcal variables as numeric as that is a different question. – Robert Long Jul 08 '21 at 14:21
  • I understood the categorical/numeric thing just browsing other SE questions and stuck with categorical. I updated the post with new questions because I tend to get overwhelmed when browsing SE questions and prefer when one post solves several issues, but can post separately if you prefer. Thank you! – answer42 Jul 08 '21 at 14:44
  • 1
    So, to *"understand the effect of `sex` while controlling for the effect of `evaluator`"* you just need to fit a model that includes both `sex` and `evaluator` plus any other competing exposures, such as age and ancestry, so the model I suggested would be appropriat for that. As for the ICC, you can calculate that directly from the mixed model. As for independence, by fitting random intercepts for individual and fixed effects for side and evaluator, we are contolling for non-independence. – Robert Long Jul 08 '21 at 17:47
  • Let us [continue this discussion in chat](https://chat.stackexchange.com/rooms/127347/discussion-between-answer42-and-robert-long). – answer42 Jul 08 '21 at 19:14