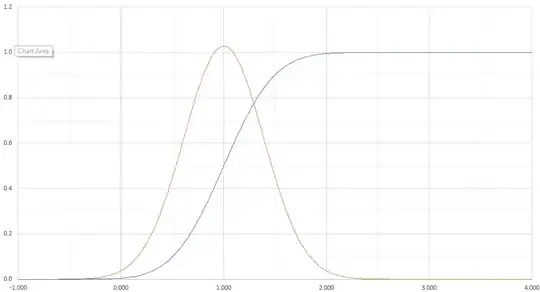
I have a normal distribution with a mean of 1. This distribution needs to have:
P(X ≤ 0) = 0.005
P(X ≤ 2) = 0.995
I've calculated the standard deviation required to achieve this as ~0.3882. I believe this is correct, as when I back calculate x ≤ 0 and x ≤ 2 for a normal distribution with the mean of 1 and the standard deviation of 0.3882, I get 0.005 and 0.995 which is what I expect.
When I plot a normal distribution with a mean of 1 and a standard deviation of 0.3882, I get probabilities greater than 1. For example, P(X = 1) = 1.028.
This seems to be saying, that X = 1 has a chance of greater than 1 ie beyond certain.
Is this correct? It does not intuitively feel right.