Wikipedia defines a weak measurement:
In quantum mechanics (and computation & information), weak measurements are a type of quantum measurement that results in an observer obtaining very little information about the system on average, but also disturbs the state very little. From Busch's theorem the system is necessarily disturbed by the measurement.
Quantum mechanics has to deal with special uncertainty considerations that classical systems (mostly) do not, but the above definition seems otherwise applicable to complex systems that may not be heavily-influenced by quantum effects. Specifically
- The observer obtains very little information about the system on average (per measurement)
- The observer does not disturb the state by much via the measurement
may be true of when we measure certain chemical, psychological, ecological, or economic systems.
A statistical view of this might be low Fisher information, or low KLD between a prior and posterior. But neither of these information quantities will tell us about how much the system has changed by our measurements.
Is there a mathematical treatment of the tradeoff between information gain and system disturbance that doesn't (necessarily) assume that quantum mechanical effects are at work?
Examples
Example 1 One example is where the original measurement is accurate when taken, but in measuring the system you have affected what future measurements of the system will be. For example, let's say you wish to measure some georeferenced physical/chemical property of deer that requires that you capture them for each measurement. Hypothetically, let's say that the deer are less likely to return to a location in which they had been caught. This would mean that future measurements of a deer may or may not have the same physical/chemical values, but will have a measurement-caused bias in the georeferenced location.
Example 2 This second example is a little more mathematically constructed. Let's say we have a real-valued random variable $X \sim \mathcal{N}(\mu, \sigma)$ that we can measure. However, we change the objects of study every time we take a measurement of them. Indexing our observations by $t \in \mathbb{N}$, our next measurement $X_{t+1}$ is distributed by $\mathcal{N}(\mu_{t+1}, \sigma)$ where $\mu_{t+1} = \mu_t + Y_t$ (note: $\mu_0$ is the original, unaffected population location) and $Y_t$ is a member of a Wiener process representing the effect of the measurement process.
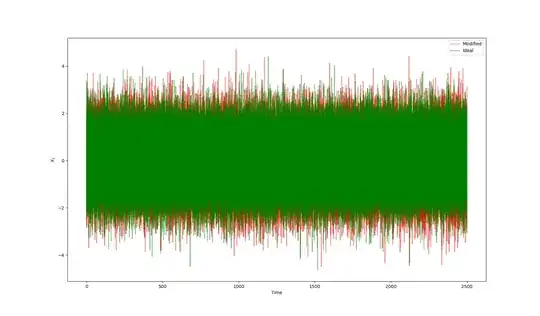
Upon further reflection I've realized that this mathematically-constructed example is not as problematic as I originally wanted to express. This is because the Wiener process has an expectation of zero, which indicates that it adds noise but doesn't cause a systemic bias. In the image below the unaffected measurement process (green) simply reflects sampling from IID standard normals, while the affected measurement process (red) is a Wiener process ($\mu=0$, $\sigma = \delta^2 dt$, $\delta=0.25$, $dt=0.1$) matching the above description.
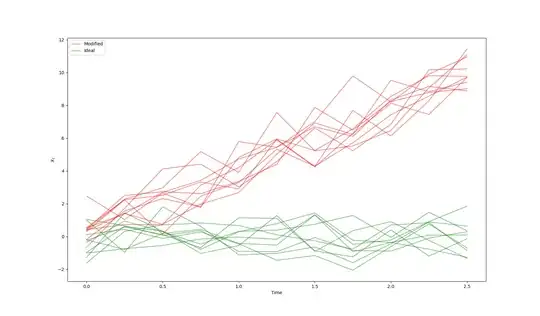
However, the introduction of a constant drift ($\mu=1$, $\sigma = \delta^2 dt$, $\delta=0.25$, $dt=0.1$) in the Wiener process illustrates an example of accumulating bias in the measurements.