This is a special case of a real symmetric quadratic form $\mathbf{x^\prime \mathbb{Q} x},$ where
$$z(x+y) + yz = xy+yz+xz= \frac{1}{2}\pmatrix{x,&y,&z}\pmatrix{0&1&1\\1&0&1\\1&1&0}\pmatrix{x\\y\\z}.$$
We find its eigenvalues $\lambda$ by solving its characteristic equation
$$p_{\mathbb Q}(\lambda) = \det\left(\mathbb{Q} - \lambda\mathbb{I}_3\right) = -\lambda^3+3\lambda+2=(\lambda-2)(\lambda+1)^2.$$
The eigenspace for $\lambda=2$ is (therefore) the kernel of
$$\mathbb{Q}-2\mathbb{I}_3 = \pmatrix{-2&1&1\\1&-2&1\\1&1&-2}$$
which evidently is generated by $(1,1,1)^\prime.$ Similarly, by inspection, we can find a basis for the two-dimensional eigenspace for $\lambda=-1.$ To match the original form I selected the first basis element to be $(1,-1,0)$ (corresponding to the linear combination $x-y,$ whose square will contribute the $xy$ term) and then chose an orthogonal vector $(1,1,-2).$ Thus, it must be the case that $xy+yz+zx$ can be written as a linear combination of the squares of $x+y+z,$ $x-y,$ and $x+y-z,$ respectively. It's now easy algebra to obtain
$$xy+yz+zx= \frac{1}{12}\left(4(x+y+z)^2-3(x-y)^2-(x+y-2z)^2\right).$$
When $(X,Y,Z)$ is standard Normal, the three squared expressions are uncorrelated (by construction) and have variances $1^2+1^2+1^2=3,$ $1^2+(-1)^2=2,$ and $1^2+1^2+(-2)^2=6,$ respectively. So, letting $U=(X+Y+Z)/\sqrt{3},$ $V=(X-Y)/\sqrt{2},$ and $W=(X+Y-2Z)/\sqrt{6},$ we have shown $(U,V,W)$ is standard Normal--all have unit variances and are uncorrelated--and that
$$XY + YZ + XZ = \frac{1}{12}\left(12 U^2 - 6 V^2 - 6 W^2\right) = U^2 - \frac{1}{2}\left(V^2 + W^2\right).$$
Finally, let the expectation of $(X,Y,Z)$ be $(\kappa,\lambda,\mu).$ By linearity, the expectation of $(U,V,W)$ is
$$E[(U,V,W)] = \left(\frac{\kappa+\lambda+\mu}{\sqrt{3}},
\frac{\kappa-\lambda}{\sqrt{2}},
\frac{\kappa+\lambda-2\mu}{\sqrt{6}}\right)$$
By definition, $U^2$ has a $\chi^2_1((\kappa+\lambda+\mu)^2/3)$ distribution and, because $V$ and $W$ are independent, $V^2+W^2$ has a $\chi^2_2((\kappa-\lambda)^2/2 + (\kappa+\lambda-2\mu)^2)/6)$ distribution. Moreover, $U^2$ is independent of $V^2+W^2$ because $(U,V,W)$ are independent. Thus,
The distribution of $XY+YZ+ZX$ is that of a $\chi^2_1((\kappa+\lambda+\mu)^2/3)$ distribution minus one-half of a $\chi^2_2((\kappa-\lambda)^2/2 + (\kappa+\lambda-2\mu)^2)/6)$ distribution.
(I haven't simplified the expressions for the noncentrality parameters in order to display their derivation.)
Arbitrary symmetric quadratic forms in Normal variables are analyzed in the same way, with comparable results: their distributions are those of linear combinations of (possibly) non-central chi-squared variables.
When the form is positive-definite, all coefficients will be positive (and vice versa).
As a check, we can generate random values in both ways. Using R, we sample from the form in the most straightforward way:
n <- 1e4
mu <- c(1,-1,3) # Mean of (X,Y,Z) -- vary at will
set.seed(17)
xyz <- matrix(rnorm(3*n), 3)
q <- xyz[1,]*xyz[2,] + xyz[2,]*xyz[3,] + xyz[3,]*xyz[1,]
The chi-squared equivalent is also simple:
ncp1 <- (mu[1] + mu[2] + mu[3])^2/3
ncp2 <- (mu[1] - mu[2])^2/2 + (mu[1] + mu[2] - 2*mu[3])^2/6
c1 <- rchisq(n, 1, ncp=ncp1)
c2 <- rchisq(n, 2, ncp=ncp2)
q. <- c1 - c2/2
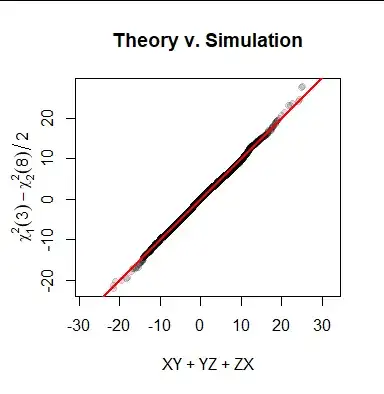
A probability plot compares the distributions:
plot(sort(q), sort(q.), asp=1,
main="Theory v. Simulation",
pch=19, col="#00000020", xlab="XY + YZ + ZX", ylab="")
mtext(bquote({chi[1]^2}(.(signif(ncp1, 2))) - {chi[2]^2}(.(signif(ncp2, 2)))/2),
side=2, line=2)
abline(c(0,1), lwd=2, col="Red")
Because the points come close to the reference line (of equal values), we see the two samples agree to within expected random deviation: