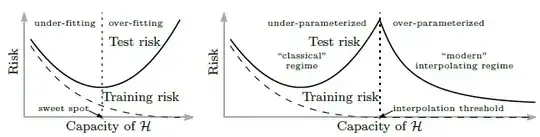
I stumbled upon the following paper Reconciling modern machine learning practice and the bias-variance trade-off and do not completely understand how they justify the double descent risk curve (see below), desribed in their paper.
In the introduction they say:
By considering larger function classes, which contain more candidate predictors compatible with the data, we are able to find interpolating functions that have smaller norm and are thus "simpler". Thus increasing function class capacity improves performance of classifiers.
From this I can understand why the test risk decreases as a function of the function class capacity.
What I don't understand then with this justification, however, is why the test risk increases up to the interpolation point and then decreases again. And why is it exactly at the interpolation point that the number of data points $n$ is equal to the function parameter $N$?
I would be happy if someone could help me out here.