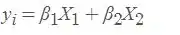Doing a t-test on a normally distributed difference of two non normal distributions

Question

I have two populations of donations (segment 2 people were subject to a different form):

              seg 1        seg 2
count   1772.000000  1645.000000
mean      93.576185   108.259574
std      301.248967   241.837942
min        3.000000     3.000000
25%       20.000000    20.000000
50%       40.000000    50.000000
75%       72.750000   100.000000
max     9000.000000  6200.000000

They don't look very normal. This is the log distribution:

But their difference does:

means = []
for i in range(0,10000):
  means.append(df_segment_1.sample(1772, replace=True).mean() - df_segment_2.sample(1645, replace=True).mean())

import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline

np.random.seed(42)

plt.hist(means, density=True, bins=30)  # density=False would make counts
plt.ylabel('Probability')
plt.xlabel('Mean difference of donations');

So I wanted to know how can I do a t-test on this population in order to know if segment 2 is significantly higher than segment 1?

Do you have a natural way of pairing your observations, such as a subject before and after a treatment? I do not follow what `means.append(df_segment_1.sample(170).mean() - df_segment_2.sample(160).mean())` means. // You say you have two populations. "Pop — Dave, Jun 22 '21 at 14:08
I'm not sure @Dave ... I have two populations of donators (segment 2 are people who were subject to a different form) — Revolucion for Monica, Jun 22 '21 at 14:11
What does the `means.append(df_segment_1.sample(170).mean() - df_segment_2.sample(160).mean())` line do? // Ignore the "population" fragment. That is a technicality not worth discussing at this time. (I'll explain later.) — Dave, Jun 22 '21 at 14:18
It compares the mean of two randomly chosen samples of 10% of each segment, @Dave . — Revolucion for Monica, Jun 22 '21 at 14:20
What you're doing with that as akin to something called bootstrap. Try sampling with the original sample sizes but with replacement. — Dave, Jun 22 '21 at 14:26
What do you mean by the original sample size @Dave ? Like the original segment size (1772 and 1645)? I tried that and it returns only one value. How do I do replacement? What does that mean? — Revolucion for Monica, Jun 22 '21 at 14:30
Yes, use the original segment sizes. // "With replacement" means that a sample of $(1,2,3,4,5)$ could be sampled as $(3,2,3,4,1)$. — Dave, Jun 22 '21 at 14:33
Ok, I did it and updated the question with the distribution of the differences, @Dave , thanks. How can do a t-test to be sure the difference is significant from there? — Revolucion for Monica, Jun 22 '21 at 14:35
You don't do a t-test on that. You do that to show that the sampling distribution of the difference in means is approximately normal, which is what the t-test requires. Now you can go do the t-test on your original data (though it does not appear that you will get a small p-value). — Dave, Jun 22 '21 at 14:38
Many thanks, @Dave , I understand now. do you have any references I could cite? In any case, should I rather use a non-parametric test like the U-test? — Revolucion for Monica, Jun 22 '21 at 14:43
There is much debate about what test to use for something like this. Frank Harrell argues to go for the Wilcoxon Mann-Whitney U test by default. I am tempted to do that, though I have found that the t-test can be quite robust in large sample sizes and that colleagues and customers are more comfortable using the familiar t-test. However you proceed, you do not go run the Wilcoxon test just because you didn't like the result of the t-test. // Efron invented/discovered bootstrap, but it is routine to appeal to the central limit theorem when you have many observations like you do. — Dave, Jun 22 '21 at 14:45

score 0 · Accepted Answer · answered Jun 30 '21 at 03:27

The resampling with replacement done is very appropriate and shows that the distribution of mean differences is close to Gaussian. This suggest that using a $t$-test is not completely misguided. We can use a $t$-test here but it is probably not our best option. On that regard, if want to use a $t$-test it will be safer to use Welch $t$-test instead of Student's $t$-test to avoid assuming equal variances.

Please note that the fact that your raw data is non-normal does not invalidate the test - as mentioned in Dave's comment we care for the difference between the two means, not the samples themselves. This has been extensively covered a couple times here. e.g. see:

That said, using Mann-Whitney-Wilcoxon rank-sum test, is a potentially better approach because it as almost as powerful (i.e. it will detect an effect if it is there) as the $t$-test if the normality assumption holds and more powerful if it does not. Somewhat simplistically, we will test of our two samples are sampled from continuous distributions with equal medians.

I would suggest reading Glen_b's exceptional answer in the thread: How to choose between t-test or non-parametric test e.g. Wilcoxon in small samples if you want some quick formal references. For a book: Nonparametric Statistical Methods by Hollander et al. is consider quite standard. If not too averse towards R, Nonparametric Statistical Methods Using R by Kloke & McKean is also very good (the R code is easy to follow, nothing crazy), I found the pace and the exposition was really nice.

Doing a t-test on a normally distributed difference of two non normal distributions

1 Answers1