As far as I know, the threshold moving is needed in imbalanced classification problems.
The reason why we have to adjust the decision threshold is as follows:
Then, I think, we do not have to adjust the discriminant threshold in a balanced classification problem.
Is it correct?
No, that is not correct.
First off, please take a look at Reduce Classification Probability Threshold, where I argue that discussions about thresholds belong to the decision stage of the analysis, not the modeling stage. Thresholds can only be set if we include the costs of misclassification - and that holds even for balanced datasets.
That thresholds are mistakenly discussed in the context of modeling is a consequence of the reliance on accuracy as an evaluation measure, which is an extremely misleading practice: Why is accuracy not the best measure for assessing classification models?
Now, to your question. We can easily simulate calibrated probabilistic predictions ("calibrated" meaning that an instance with a predicted probability $\hat{p}$ of belonging to the target class actually belongs to the target class with probability $p=\hat{p}$, so we are not dealing with artifacts of mispredicting) for a balanced dataset, simply by drawing predictions $\hat{p}_i\sim U[0,1]$, then assigning instance $i$ to the True class with probability $\hat{p}$. Now, using a threshold $t$ amounts to treating instance $i$ as True if $\hat{p}_i>t$, and as False if not.
What is an "optimal" threshold? This will, as above, depend on the costs of misclassification. Whether you treat a True as False, or a False as True, may have very different costs indeed. And this holds even for balanced datasets. If the costs of treating a False as True and much higher than the reverse costs of treating a True as False, then it makes sense to increase the (decision!) threshold.
As an example, perhaps you have a database of people that you may want to sell something to. If you do not offer the product to someone who would have bought it (treating a True as False), you lose the sale. If you offer the product to someone who does not want it (treating a False as True), you may send this person unwanted emails, and majorly tick them off. Thus, the costs are asymmetric. It only makes sense to pitch your product to people where you are highly certain they will buy it (and not be ticked off), i.e., you want to choose a high decision threshold.
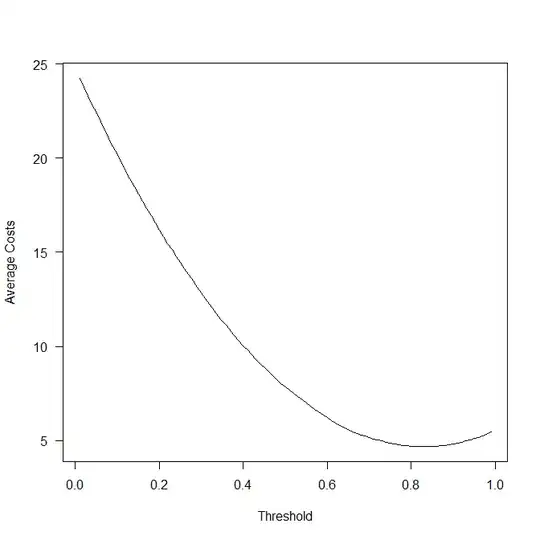
Below, I make some assumptions on the relevant costs and simulate the costs depending on the threshold. As you see, the lowest-cost threshold is definitely not at 0.5. This is R code; you can adapt and run it yourself as you see fit.
cost_of_treating_T_as_T <- 0 # incurred if outcome==T & probabilities_of_T>=threshold
cost_of_treating_T_as_F <- 10 # incurred if outcome==T & probabilities_of_T<threshold
cost_of_treating_F_as_T <- 50 # incurred if outcome==F & probabilities_of_T>=threshold
cost_of_treating_F_as_F <- 1 # incurred if outcome==F & probabilities_of_T<threshold
nn <- 1e5
probabilities_of_T <- runif(nn)
outcomes <- runif(nn)<probabilities_of_T
sum(outcomes)/nn # balanced data
thresholds <- seq(.01,.99,by=.01)
average_costs <- sapply(thresholds,function(tt)
cost_of_treating_T_as_T*sum((probabilities_of_T>=tt)*outcomes) +
cost_of_treating_T_as_F*sum((probabilities_of_T<tt)*outcomes) +
cost_of_treating_F_as_T*sum((probabilities_of_T>=tt)*(!outcomes)) +
cost_of_treating_F_as_F*sum((probabilities_of_T<tt)*(!outcomes))
)/nn
plot(thresholds,average_costs,type="l",las=1,xlab="Threshold",ylab="Average Costs")
Finally, my answer to Example when using accuracy as an outcome measure will lead to a wrong conclusion discusses this situation from a closely related angle.
