3

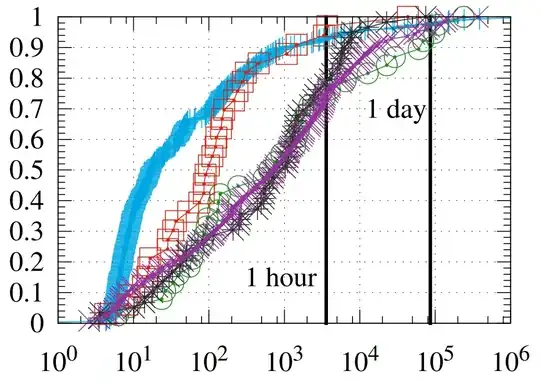
I've been reading this very nice paper by Baltrunas et al. and I would like to have a distribution that looks as much as possible like the empirical data the authors found in the figure below:

enter image description here

I don't have access to the data and it doesn't have to be exact, so I've modeled the green, purple and black lines with a lognormal distribution (s=2, loc=0, scale=10^3) which looks like this:

enter image description here

However, I can't find a distribution that behaves like the blue line. The line looks like an exponential CDF pattern but the x axis is in log scale. Is there a known distribution which I can use as reference for this case?

Thanks in advance.

Gabriel Rebello
  • 131
  • 1
  • My post at https://stats.stackexchange.com/a/35717/919 describes a simple procedure that is likely to work well in your example: estimate a Box-Cox transformation with a "start value" or "offset" of around 0.8 on a common log scale. Work with the logarithms of the data throughout, converting back to the original values only at the end. – whuber Jun 10 '21 at 12:39
  • Thanks @whuber. Maybe I lack the knowledge, but I couldn't find a good fit using Box-Cox. I used the three-point method with x = [ 1e1, 1e2, 1e6] and y = [0.4, 0.7, 1] but I can't find good lambda/alpha values that make boxcox reasonably map x to y. – Gabriel Rebello Jun 16 '21 at 15:40
  • You need to fit the *logs* of $x$ against $y.$ Try a Box-Cox parameter of $-1$; that is, look for a relation of the form $y=\alpha+\beta / ({\log}_{10}x).$ A value of $-1/2$ will work better for smaller $x$ but not as well for larger $x:$ use your judgment to fit the data within the most useful range for your application. – whuber Jun 20 '21 at 17:42

1 Answers1

0

We can approximate the blue line by a quarter-ellipse with center at $(10^6,0)$, major axis going through $(10^{0.5}, 0)$ and minor axis going through $(10^6, 1)$. This leads to the equation $$F(x)=\sqrt{1- \left(\frac{\log(10^6/x)}{\log(10^{5.5})}\right) ^{\!\!2}}$$ Using $\log$s in base $10$, this leads to a pdf of $$f(x)= \frac{(6-\log x)/5.5}{x\sqrt{5.5^2 - (6-\log x)^2}}$$ for $\sqrt{10} < x < 10^6$, and zeroes outside that range.

Matt F.
  • 1,656
  • 4
  • 20