What does the logit value actually mean?

Question

I have a logit model that comes up with a number between 0 and 1 for many cases, but how can we interprete this?

Lets take a case with a logit of 0.20

Can we assert that there is 20% probability that a case belongs to group B vs group A?

is that the correct way of interpreting the logit value?

In addition to @SvenHohenstein's good answer below, it may help you to read my answer here: [Interpretation of simple predictions to odds ratios in logistic regression](http://stats.stackexchange.com/questions/34636//34638#34638), which contains additional basic information about probabilities & odds. Note that the logit can be understood more abstractly as a link function; you can read more about that here: [difference-between-logit-and-probit-models](http://stats.stackexchange.com/questions/20523//30909#30909) (although this answer might be a bit more technical). — gung - Reinstate Monica, Mar 20 '13 at 23:08
I want to know why the pronunciation of *logit* is neither like *logarithm* nor like *logistic* — Henry, Nov 15 '13 at 01:14
@Henry - According to Wiktionary, the U.S. pronunciation of 'logit' /ˈloʊdʒɪt/ (https://en.wiktionary.org/wiki/logit) is like 'logistic' (/loʊˈdʒɪs.tɪk/) (https://en.wiktionary.org/wiki/logistic). — shaneb, Feb 08 '19 at 22:39
@shaneb - fair enough - thought that only shifts the question to the un*logical* pronounciation of *logistic* — Henry, Feb 10 '19 at 20:38

score 67 · Answer 1 · edited Nov 15 '13 at 01:04

67

The logit $L$ of a probability $p$ is defined as

$$L = \ln\frac{p}{1-p}$$

The term $\frac{p}{1-p}$ is called odds. The natural logarithm of the odds is known as log-odds or logit.

The inverse function is

$$p = \frac{1}{1+e^{-L}}$$

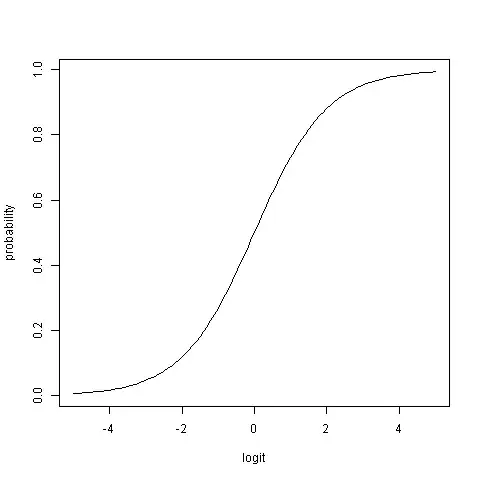
Probabilities range from zero to one, i.e., $p\in[0,1]$, whereas logits can be any real number ($\mathbb{R}$, from minus infinity to infinity; $L\in (-\infty,\infty)$).

A probability of $0.5$ corresponds to a logit of $0$. Negative logit values indicate probabilities smaller than $0.5$, positive logits indicate probabilities greater than $0.5$. The relationship is symmetrical: Logits of $-0.2$ and $0.2$ correspond to probabilities of $0.45$ and $0.55$, respectively. Note: The absolute distance to $0.5$ is identical for both probabilities.

This graph shows the non-linear relationship between logits and probabilities:

enter image description here

The answer to your question is: There is a probability of about $0.55$ that a case belongs to group B.

edited Nov 15 '13 at 01:04

Nick Cox

48,377
8
110
156

answered Mar 20 '13 at 16:51

Sven Hohenstein

6,285
25
30
39

*" Logits of $-0.2$ and $0.2$ correspond to probabilities of $0.45$ and $0.55$ respectively."* How does it imply that logit distribution is symmetric? – user 31466 Feb 12 '15 at 03:50
*There is a probability of about $0.55$ that a case belong to group B.* When will it belong to group A ? – user 31466 Feb 12 '15 at 03:55
2

@Leaf Since there are only two groups, A and B, the probability for group A is $1 - 0.55 = 0.45$. – Sven Hohenstein Feb 12 '15 at 06:59
1

@Here, symmetry is related to the *absolute difference* to a probability of $0.5$ or a logit of $0$. If probability is $0.5 + x$, the logit is $0 + y$; If probability is $0.5 - x$, the logit is $0 - y$. Here, $\text{sign}(x) = \text{sign}(y).$ – Sven Hohenstein Feb 12 '15 at 07:02

score 3 · Answer 2 · answered Dec 01 '20 at 21:03

To add a more modern (but not very deep) perspective, consider how it's used in deep learning (ha, pun intended...):

logit is referred to the output of a function (e.g. a Neural Net) just before it's normalization (which we usually use the softmax). This is also known as the code. So if for label $y$ we have score $f_y(x)$ then the logit is:

$$ logit = \log \left( \frac{ e^{f_y(x)} }{Z} \right) = score = f_y(x)$$

Where $Z$ is the standard partition function. By the way, this is all over the place in the pytorch and tensorflow documentation.

So you can interpret it as:

the (unnormalized) score for a label or (functional confidence) for a specific class/label.

One of the many references: https://stackoverflow.com/questions/41455101/what-is-the-meaning-of-the-word-logits-in-tensorflow

score 0 · Answer 3 · answered Mar 20 '13 at 15:59

Could you maybe specify your model and give a screenshot of the output, then I could give you an detailed answer, but as a first try.... you may want to check out also the following examples on these websites:

http://www.ats.ucla.edu/stat/stata/seminars/stata_logistic/default.htm

http://www.ats.ucla.edu/stat/stata/dae/logit.htm

http://www.ats.ucla.edu/stat/stata/faq/oratio.htm

http://www.ats.ucla.edu/stat/mult_pkg/faq/general/odds_ratio.htm

so if the coefficient is 0.2 it depends on the variable, I guess you have a dummy, which is e.g. 0 for group B and 1 for group A?

odds ratio is given by: $OR = e^b$

so in your case: $e^{70.20}$

This would be the odds ratio of your group variable corresponding to your reference group.