I have a Latent variable model like this
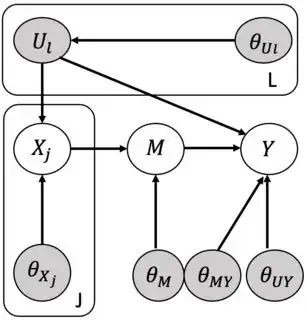
White nodes are observed and gray nodes are latent. $\theta = \{\theta_U, \theta_X, \theta_M, \theta_{MY}, \theta_{UY}\}$ are the parameters of this model that we treat as random variables and define a prior distribution over them. We use an inference algorithm like Hamiltonian Monte Carlo (HMC) or Stochastic Variational Inference (SVI) to learn a posterior distribution $\Pi(\theta|\text{observed data})$ over the parameters. Assume that the ground truth parameters that the training data is generated from are $\theta^*$ and the joint distribution over the training data is $P(x^*, m^*, y^*)$. Given $\Pi(\theta|x^*, m^*, y^*)$, we start generating data by repeating this process: $$ \theta \sim \Pi(\theta|x^*, m^*, y^*)\\ u \sim P(U|\theta_U) \\ x \sim P(X |u, \theta_X)\\ m \sim P(M | x, \theta_M) \\ y \sim P(Y | m, u, \theta_{MY}, \theta_{UY}) $$ Can we say that the joint distribution $P(x,m,y)$ is the same as the joint distribution $P(x^*, m^*, y^*)$? Is there any guarantee for this depending on the inference algorithm or any other assumptions?