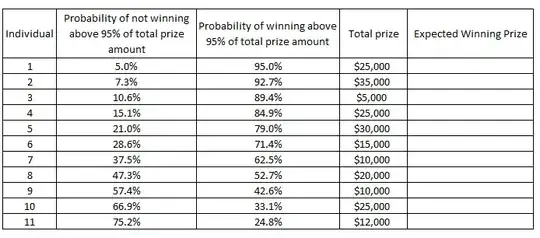
For this probability model, As I am new to probability, I am looking for an approach of the underlying probability concept to work on the calculation in arriving at the expected winning prize of the total prize amount based on the Probability of not winning above 95% of the total prize and the Probability of winning above 95% of the total prize for each individual from my side.
I need an approach or any paper link on the model of this approach and not a final solution or entire calculation for this problem.
The expected winning prize amount should be based on both probabilities. Looking for a concept and not an actual final calculated number
Can I define the expected value of integral survival function as below ?
$\mathbb{E}Y=\int_{0}^{\infty}1-F_{Y}\left(x\right)dx$