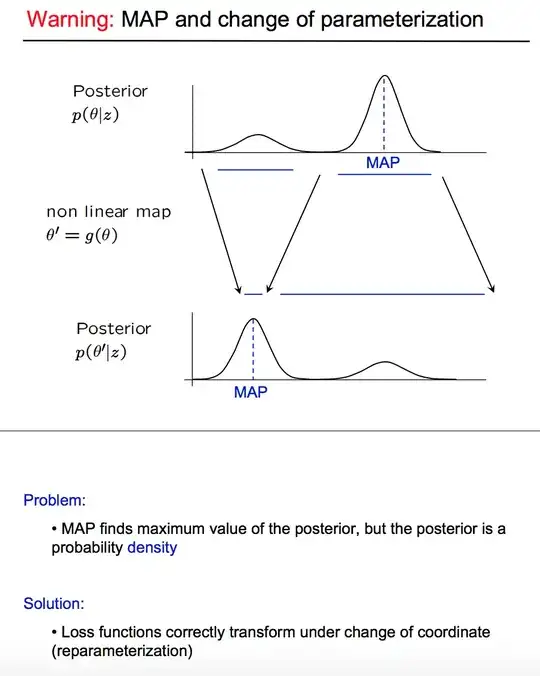
I learned why MAP suffers from being reparametrization invariance while MLE not from this answer, but I don't know why reparametrization invariance even matters? What is the non-linear mapping concretely and why we do the non-linear mapping depicted below?
I wonder if I am wrong: After we obtain the posterior we can provide a point estimate summary, such as mean, median, and mode if necessary. In which scenarios do we apply non-linear mapping to the posterior? For the sake of what?
I learned from this section in this book that:
We will now show that different parameterizations can pick different points in this interval arbitrarily.
But it is unclear why we apply the parameterization to the MAP. Any materials(tutorials) would also be very appreciated.