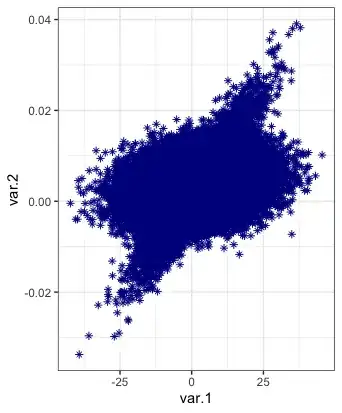
I have two variables that are supposed to correlate with each other across the whole dataset, but as you can see in the scatter plot below, it appears that I have a mix of two sub-samples.
One in which the variables correlate perfectly with each other (i.e. data points falls on the regression line) and a bigger chunk in which the two variables are not correlated as much.
I'd like to select data points for which the two variables correlates perfectly which other. I tried to fit a simple regression line and remove outliers based on cook's distance > 4/n. (see the scatter plot below)
Also tried singular value decomposition to no avail!
This should be pretty basic with numerous ways to resolve it; Still I am wondering what would be the best approach for selecting only data points with perfect correlation across the two variables. Any ideas in R or python is much appreciated!