0

I'm fairly new to time series analysis and forecasting. I'm using the uci househould power consumption dataset to build a model to forecast energy consumption.

The dataset measures the power (kW) averaged during a 1 minute period, but I'm interested in energy (kWh), so I divide by 60 and I resample to change the frequency to hours.

power_consumption['Global_active_power'] = power_consumption['Global_active_power'].apply(lambda x: x/60)
power_consumption=power_consumption.resample('h').sum()

Once, I have the dataset the way it fits my needs I want to check if the time series is stationary, and then is where I'm getting confused.

When I run the ADFuller test I get the following:

result = adfuller(power_consumption['Active_Energy'])
print(f'ADF Statistic: {result[0]}')
print(f'p-value: {result[1]}')
for key, value in result[4].items():
    print('Critial Values:')
    print(f'   {key}, {value}')    

ADF Statistic: -14.279731281927612
p-value: 1.3303299942732509e-26
Critial Values:
   1%, -3.4305393559398922
Critial Values:
   5%, -2.8616236906108443
Critial Values:
   10%, -2.566814545887977

So, having such p-value is fair to assume that the time series is stationary, right?

Then I plot the ACF and PACF and I get the following:

lag=240
plot_acf(power_consumption['Active_Energy'],lags=lag )
pyplot.show()

enter image description here

plot_pacf(power_consumption['Active_Energy'],lags=lag )
pyplot.savefig('PACF.jpg')

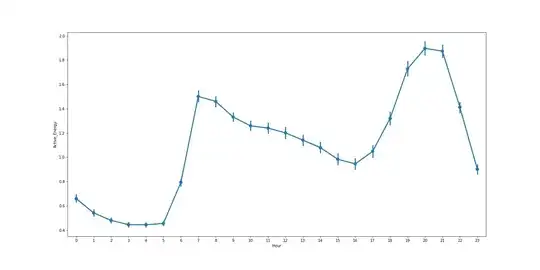
enter image description here

But as you can see ACF and PACF plots represent a seasonal behavior, which makes sense because during the data exploration I could see that the energy consumption has a seasonal pattern during the year and during the day. As it is shown in the plots below.

enter image description here enter image description here

So my questions are the following:

Can the data be seasonal and stationary? It has been discussed here but I don't get it.

Is the data 'seasonal' enough, if that makes sense, to apply SARIMA or should I go for ARIMA?

If I should apply ARIMA, how can I tune the parameters p,d,q from the ACF and PCF?

Armen Firman
  • 1
  • 1
  • 1
    I see why that thread is confusing. A seasonal process is not stationary. Full stop. This is a trivial consequence of the definitions: seasonality is a regular change in the marginal distribution while stationarity is the absence of change (of any kind) in the marginal distribution. Everything else in that thread is picking at a finer point, which is that one may (in various senses) *remove* forms of seasonality, to leave a stationary residual process. – whuber May 25 '21 at 20:00
  • @whuber Thank you for answering!! My point is I think my dataset is seasonal, therefore should be non-stationary. But, when I apply the ADFuller test I get a low p-value, correct me if I'm wrong, which means the time series is stationary. So, I should trust the ADFuller test even though I appreciate non-stationary behaviour? – Armen Firman May 25 '21 at 21:25
  • You seem to be confusing yourself, because in the post you stated (correctly) the opposite: "So, having such p-value is fair to assume that the time series is non-stationary, right?" Right. – whuber May 25 '21 at 21:31
  • @whuber Sorry my mistake. I meant that the time series is stationary. I did the test and I got a e-26 p_value, wich is well below the 0,05 mark, which makes reasonable to assume that the time series is stationary. Sorry for being a bit messy, as I said I'm fairly new to time serie. – Armen Firman May 25 '21 at 21:49
  • The low p-value *rejects* the hypothesis of stationarity. In this case it restates the obvious: your series isn't remotely stationary. – whuber May 25 '21 at 22:36
  • @whuber In the ADF test, the null hypothesis is that there is a unit root; low p-value rejects this in favor of a stationary AR process. I think the actual issue here is that the lag order is too low (it would need to be roughly on the order of the seasonal period), so that the test statistic doesn't have the stated distribution and the p-value is meaningless. – Chris Haug May 26 '21 at 01:29
  • @ChrisHaug What do you mean by lag order? And why we should consider the p-value meaningless? – Armen Firman May 26 '21 at 06:55
  • ADF test is based on a regression that includes lags of differences up to some maximum order. You have to choose this to be high enough so that the residuals are white noise, because if they aren't then the test statistic does not have the right distribution, the critical values are wrong and so the p-value is as well. It doesn't look like you pass in a value for it so you should check the documentation for whatever software you're using to see what it sets as a default, and what it has picked in this instance. – Chris Haug May 26 '21 at 11:38
  • @Chris Thank you for setting me straight on that. – whuber May 26 '21 at 12:49
  • @ChrisHaug Thank you for the information! I looked at the documentation and, yes, there is a parameter for setting the lag. And now I have a new question, which value should I use? 24 because of the daily seasonality or 8760 because of the yearly seasonality. If I use 24 I get an even smaller p-value, and I cannot use 8760 because my computer collapses (currently I'm hipertunning a neural network). – Armen Firman May 26 '21 at 21:40

0 Answers0