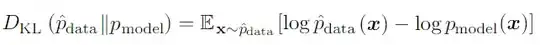Self-normalized weighted sum of random variables

Question

Given $n$ i.i.d. random variables $X_1, \dots, X_n$ with $X_i \sim \mathcal{N}(0,1)$ and weights $a_1, \dots, a_n \in [-1, 1]$ such that

$$ Y = \frac{P}{Q} = \frac{\sum_{i = 1}^{n} a_i X_i }{\sum_{i = 1}^{n} X_i} $$

Thus, the numerator is $P = \sum_{i = 1}^{n} a_i X_i \sim \mathcal{N}(0,\sum_{i = 1}^{n} a_i^2)$ and $Q = \sum_{i = 1}^{n} X_i \sim \mathcal{N}(0,n)$.

I like to learn more background on Y; in particular, I'm interested in some closed-form approximation or bounds of Y based on the weights. . However, I don't know how to handle the fraction. I have found few papers which call $Y$ a self-normalized weighted sum; however, this seems to be not a common terminology as self-normalization typically refers to $\sum_{i = 1}^{n} X_i / \sum_{i = 1}^n X_i^2$.

Could you please expand on what you mean by "I would like to determine Y" — Ariel, May 23 '21 at 16:35
@Ariel : Essentially I’m looking for some theory on Y, eg, a closed form expression or applicable limit theorem. — Sebastian Schlecht, May 23 '21 at 17:36
I’m particularly interest in some closed form approximation or bounds of Y based on the weights. — Sebastian Schlecht, May 23 '21 at 17:39
Not really, although they are typically between -1 and 1. For one application, a_i are also normalized vectors, but that might be more difficult. — Sebastian Schlecht, May 23 '21 at 17:44
For one thing, the numerator and denominator of $Y$ are jointly normal. If we assume $X_i$'s to have zero means, then it would have a [Cauchy distribution](https://en.wikipedia.org/wiki/Ratio_distribution#Correlated_central_normal_ratio). It would be easier to answer if you add more details by editing your post. — StubbornAtom, May 23 '21 at 19:00
@StubbornAtom The ratio distribution is a great lead. Yes, we can assume zero means. If I understand correctly, we need to determine the correlation between the numerator and denominator from the weights. — Sebastian Schlecht, May 23 '21 at 19:23
Yes, and using this I think you get the neat result $Y\sim \text{Cauchy}(\overline a,s_a)$ as @whuber elaborates, where $s_a$ is the standard deviation of the $a_i$'s. Provided of course $a_i\ne 1$ for at least one $i$. — StubbornAtom, May 23 '21 at 21:17

whuber · Accepted Answer · 2021-05-23T20:31:27.527

Because $(P,Q)$ is a linear transformation of $(X_1,\ldots, X_n),$ it has a binormal distribution. Its mean is $(0,0)$ and its covariance matrix is determined from the bilinearity of covariance,

$$\operatorname{Cov}(P,Q) = \pmatrix{\sum a_i^2 & \sum a_i \\ \sum a_i & n}.$$

Let's regress $P$ against $Q:$ that is, let's find a variable $Z$ where $P = \beta Q + Z$ and $Z$ is uncorrelated with $Q.$ This gives the equation

$$0 = \operatorname{Cov}(Z, Q) = \operatorname{Cov}(P-\beta Q, Q) = \sum a_i - \beta n$$

with unique solution

$$\beta = \frac{1}{n}\sum_{i=1}^n a_i = \bar a,$$

whence

$$Z = P - \beta Q = P - \bar a Q,$$

implying

$$\operatorname{Var}(Z) = \operatorname{Var}(P - \bar a Q) = \sum_{i=1}^n a_i^2 - 2\bar a n + (\bar a)^2 n = n \operatorname{Var}(a).$$

Use this to rewrite the fraction in the form

$$\frac{P}{Q} = \beta + \frac{Z}{Q}.$$

The fraction obviously is a multiple of the ratio of uncorrelated (and therefore independent) standard Normal variables with the multiple equal to the standard deviation of the $a_i.$ It is well known (and easy to show that the ratio of independent standard Normals has a Cauchy distribution (aka Student's t with 1 degree of freedom).

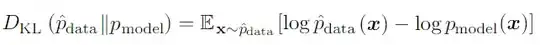
This figure is a histogram of 100,000 draws of $Y=P/Q$ where $n=15,$ $\bar a = 0.52,$ and $\operatorname{SD}(a) = 0.31.$ (Approximately 4% of the values drawn would not fit on the horizontal axis. As a result, the plotted densities of the histogram and red curve are all about 4% too large; but that's ok for these comparisons.) Over it I have drawn the shifted, scaled Cauchy distribution in red. For comparison, the graph of a standard Cauchy distribution is shown as a dotted black curve. The agreement of the red curve with the histogram suggests this solution is correct.

This is the R code to produce the figure.

n <- 15
#
# Generate a random set of weights.
#
set.seed(17)
a <- runif(n, 0, 1) # (Limiting to positive values will make beta clearly nonzero)
#
# Generate many values of Y.
#
n.sim <- 1e5
X <- matrix(rnorm(n*n.sim), n.sim)
P <- X %*% a
Q <- X %*% rep(1, n)
Y <- P/Q
#
# Plot the distribution of those values as a histogram.
#
i <- abs(Y) <= 5
Y <- Y[i]
hist(Y, freq=FALSE, col="#f0f0f0", breaks=100)
#
# Compare the histogram to the theoretical solution.
#
beta <- mean(a)                   # The mean of the weights
sigma <- sqrt(mean((a - beta)^2)) # The SD of the weights
curve(dt((x-beta)/sigma, 1)/sigma/mean(i), n=1001, add=TRUE, lwd=2, col="Red")
abline(v=beta, lwd=2) # Mark the center of this distribution
#
# Draw a Cauchy PDF for reference.
#
curve(dt(x, 1), n=1001, add=TRUE, lwd=1,lty=3)

Self-normalized weighted sum of random variables

1 Answers1