A coin with probability of heads $p \in (0, 1) $ is tossed $n$ times. What is the joint probability distribution of the number of runs and the longest run?
Schilling (1990) discusses the distribution of the longest run but I haven't found a good source for the joint distribution of the longest run and the number of runs. I also found this post at Mathematics Stack Exchange.
As an illustration, I've randomly generated 10 coin tosses with a fair coin ($p=0.5$) and got the following sequence: $\text{TTHTHHTTHT}$. The longest run is 2 and the number of runs is 7.
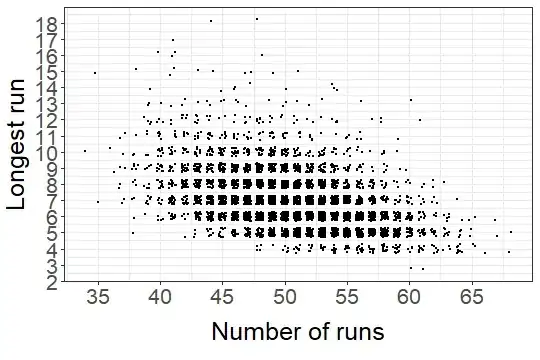
Here is a simulation with 5000 repeats using $n=100$ and $p=0.5$: