What distributions have an undefined mean but are not symmetric?

Question

What distributions have an undefined mean but are not symmetric?

I'm looking for a probability distribution function (and CDF) for which the mean is undefined, but not symmetric like Cauchy, but a positive, continuous probability distribution with infinite mean and with a maximum density away from zero -- shaped like Poisson with a "hump".

I think a fat tail to positive infinity should work for an undefined mean, but what distributions are like that?

Answer 1

I am guessing that you are looking for a positive, continuous probability distribution with infinite mean and with a maximum density away from zero.

I thought that by analogy with a Gamma distribution ($p(x) \propto x^a \exp(-x) \, dx$), we could try something with a rational (polynomial) rather than an exponential tail. After a little bit of lazy R and Python (sympy) experimentation, I came up with

$$ p(x) = \frac{1}{2\sqrt{3}\cdot \pi/9} \cdot \frac{x}{1+x^3} \, dx $$

(I initially tried $p(x) \propto x/(1+x^2)$, but its integral diverges.) $\int_0^\infty p(x) \, dx$ is 1, as required, and $\int_0^\infty x p(x) \, dx$ diverges.

I don't know if this distribution has a name/literature associated with it.

The CDF is available in closed form but is pretty horrible ... (see Python code below ...)

$$ 3 \sqrt{3} \left(- \frac{\log{\left(X + 1 \right)}}{6 \pi} + \frac{\log{\left(X^{2} - X + 1 \right)}}{12 \pi} + \frac{\sqrt{3} \operatorname{atan}{\left(\frac{2 \sqrt{3} X}{3} - \frac{\sqrt{3}}{3} \right)}}{6 \pi}\right) + \frac{1}{4} $$

Without actually trying anything, I would guess that distributions of the form $x^a/(1+x^{a+2})$ will generally have these properties (but the computations will get progressively nastier). Someone with more analysis skills could probably prove a bunch of things.

---

An extremely knowledgeable colleague identified this as almost the same as a "Beta-Type 2 (m=2/3,n=1/3)" distribution (a Beta-Type 2 distribution has a term of the form $(1+x)^n$ in the denominator rather than the $1+x^n$ given above). You might want to use the Beta-Type 2 instead of my version; since you know what it's called you can search for useful code, or literature on its properties (e.g. here or here or McDonald et al 2013), or cite it in a paper: "Beta-Type 2" sounds so much better than "a distribution that some guy on CrossValidated made up".

... the Beta-Type 2 family with its density as

$$ f(x) = \frac{1}{\textrm{Beta}(m,n)} \frac{x^{m-1}}{(1+x)^{m+n}} $$

over the support $(0,\infty)$

It is evident that if $m$ is chosen to be > 1, the mode will be away from 0. Also, if $n$ is chosen to be $\leq 1$, then the mean will be infinite. This family will produce [an] uncountable number of models with the property you are looking for. ... If you set $Y=X^3$ in your model, then it becomes a Beta-Type 2 $(m=2/3,n=1/3)$ and you can see that this fits the description I have given above.

They also identified the name of @ThomasLumley's contribution:

... it is called power gamma model or exponential-gamma model.

---

McDonald, James B., Jeff Sorensen, and Patrick A. Turley. “Skewness and Kurtosis Properties of Income Distribution Models.” Review of Income and Wealth 59, no. 2 (2013): 360–74. https://doi.org/10.1111/j.1475-4991.2011.00478.x.

---

R code:

f <- function(x) 1/(2*sqrt(3)*pi/9)*x/(1+x^3)
integrate(f, 0, Inf) ## 1 with absolute error < 4e-07
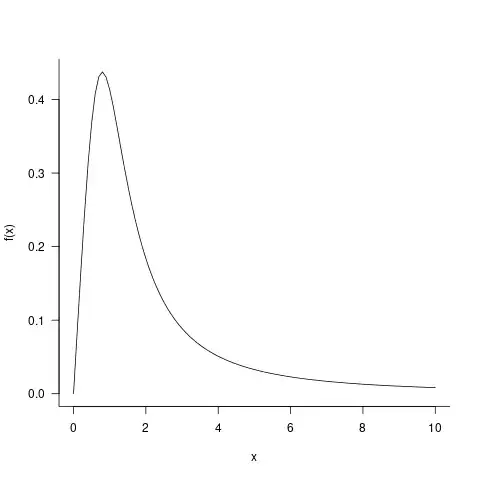
curve(f, from=0, to=10)

Python code (because I'm too lazy to integrate):

from sympy import *
x, n, N = symbols('x,n,N')
n=integrate(x/(1+x**3), (x, 0, oo))    ## 2*sqrt(3)*pi/9
integrate(x**2/(1+x**3), (x, 0, oo)) ## infinite mean
cdf = integrate(1/n*x/(1+x**3), (x, 0, X))
print(latex(cdf))

Answer 2

If $X$ comes from Gamma distribution with pdf $$f(x) = \frac{1}{\Gamma(k)}x^{k-1}e^{-x}$$ then $E[\exp(tX)]$ (the moment-generating function) exists only for $t<1$, so $Z=\exp(X)$ (or even $Z-1$) is a strictly positive random variable without a finite mean. For $k>1$ the mode is not at the lower limit

Answer 3

Pareto distribution with density $$ f(x) = \begin{cases} \frac{\alpha m^\alpha}{x^{\alpha+1}} &, x\ge m \\ 0 &, x<m \end{cases} $$ for some parameters $m>0, \alpha>0$. When $\alpha > 1 $ the expectation exists and is given by $\frac{\alpha}{\alpha-1}\cdot m$. When $\alpha \le 1$ the expectation do not exist, or as we say, it is infinite, because the integral defining it diverges to infinity.

Details in my answer at What is the difference between finite and infinite variance

Answer 4

I'll focus on continuous RVs. Let $X$ be a RV supported on $\mathbb R$ with density $f$.

If $X \geq 0$ a.s. (or $X\leq0$ a.s.) then the mean is well-defined, it's just $+\infty$ (or $-\infty$ if negative). This is just like how a sum of non-negative things always converges, it just might converge to $+\infty$. An example of this is the folded Cauchy distribution. In order to have an undefined mean we need $X$ to take both positive and negative values, and the mean on either set of values need to be infinite so that there's no overall mean.

Here's an example: take $$ f(x) \propto \begin{cases} \frac 1{(x-1)^2+1} & x < 1 \\ \frac 1{(x-1)^{3/2}+1} & x \geq 1 \end{cases} $$ Then $$ \text EX = \int_{-\infty}^\infty xf(x)\,\text dx \propto \int_{-\infty}^1 \frac{x}{(x-1)^2+1}\,\text dx + \int_1^\infty \frac{x}{(x-1)^{3/2}+1}\,\text dx = -\infty + \infty $$ and this is undefined. I'm just combining two different tails where both are integrable but neither has a finite first moment. I'm also shifting it over to get the mode away from zero.

Answer 5

A non-central F-distribution with $\nu_1=\nu_2=2$ degrees of freedom and non-centrality shape parameter $\lambda=3$ has support on $\mathbb{R}^+$ and looks like it satisfies all your requirements. Beta functions and Gamma functions have been expanded to put it in this very simple form:

$$ f(x)=\frac{e^{-\frac{3}{2 x+2}} (5 x+2)}{2 (x+1)^3}, \ x\ge0 $$ The CDF is very simple too: $$ F(x)=\frac{e^{-\frac{3}{2 x+2}} x}{x+1} $$ We have the following: $$ \int^\infty_0{f(x)\ \text{d}x} = \displaystyle\lim_{x \to \infty}\frac{e^{-\frac{3}{2 (x+1)}} x}{x+1}=1 $$ The mean doesn't exist when $\nu_2\leq2$, and neither does the variance when $\nu_2\leq4$ which is our case above.

The mode appears at $x=(-7 + 3 \sqrt{41})/40\approx0.305$ so it has a maximum density beyond $0$.

Answer 6

One of the Pareto distributions: \begin{align} & \Pr(X>x) = \frac 1 x \text{ for }x\ge1. \\[8pt] & \Pr(X\in A) = \int_A \frac{dx}{x^2} \text{ for } A\subseteq (1,+\infty). \end{align}

Answer 7

The St. Petersburg distribution: $$ \Pr(X= 2^n) = \frac 1 {2^{n+1}} \text{ for } n = 0,1,2,3,\ldots $$