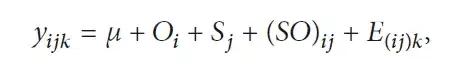Suppose I have a y vs. x data as in
x,y
1, 14.75
2,11.18
3,21.72
...
19,71.17
20,73.10
Using Matlab's cftool, and a linear fit model, I get $y=ax+b$ where $a=a_0+\Delta a$ and $b=b_0+\Delta b$.
The $y=a_0 x+b_0$ function fits nicely to this data (red curve in the image).
But I am interested in plotting a fit to this data which also takes into consideration the error of the parameters $a$ and $b$, namely $\Delta a$ and $\Delta b$.
Is it correct to say that the error of the fit are the lines
$y=(a_0+\Delta a)x+(b_0+\Delta b)$
and
$y=(a_0-\Delta a)x+(b_0-\Delta b)$ (black in image)?
These two lines are the extreme case when we are on the end of the error (in the + and - direction) for both $a$ and $b$.
I guess that answer is no, and I would like to have an explanation why.
If no, then what is the correct way to mark up graphically the error of this fit?
More generally, how would I establish this method for a more complicated fit function, such as a Lorentzian ($\frac{A^2}{(x-u)^2+\gamma^2}$) which has 3 parameters -
$A_0+\Delta A$, $u_0+\Delta u$ and $\gamma_0+\Delta \gamma$?