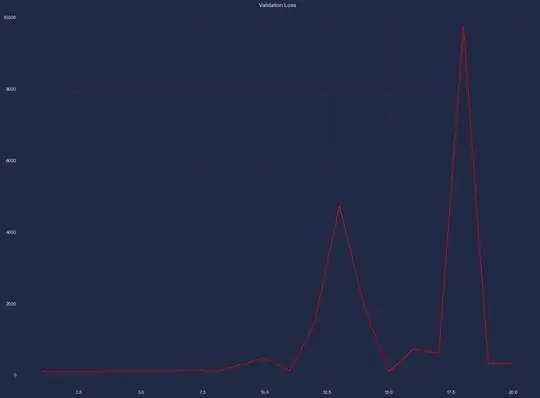
Let's say I have a sample of one million observations that each get a score of 0-1. I would like to use the average score in the sample as an estimate for its true value in the population.
To get the 95% confidence interval, I would use a formula like:
Where the sample standard deviation (sigma) is equal to:
Isn't it strange that the confidence interval is the same regardless of whether the true population size is 1,000,001 or one billion? My gut would say we should a wider bandwidth for the 95% confidence interval if we know the population is one billion instead of 1,000,001. But the formulas above don't account for this.
Is there a solution to this paradox?