I just have 1500 data points in excel. However, I want to do a chi squared test to prove if the data is normaly distributed.
My question is: How to calculate the expected range for such a large data set?
UPDATE
How to calculate the relative frequencies for such a large data set?
1) No test will prove your data is normally distributed. In fact I bet that it isn't.
(Why would any distribution be exactly normal? Can you name anything that actually is?)
2) When considering the distributional form, usually, hypothesis tests answer the wrong question. What's a good reason to use a hypothesis test for checking normality?
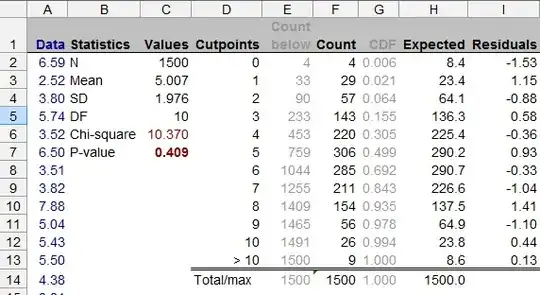
I thought that the chi squared test or the Kolmogorov–Smirnov test provide a good indication about the distribution.
However, if not, what are some usecases they are good for?
I can think of a few cases where it makes some sense to formally test a distribution. One common use is in testing some random number generating algorithm for generating a uniform or a normal.
3) If you want to test normality, a chi-squared test is a really bad way to do it. Why not, say, a Shapiro-Francia test or say an Anderson-Darling adjusted for estimation? You'll have far more power.
4) What do you mean by 'expected range', specifically?
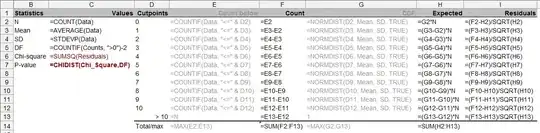
by expected range I mean in the formula of the chi squared test the relative frequencies: ei=n∗pi
To have expected counts you need to split it up into subranges, and multiply the total count by the probability in the subrange.
Using a spreadsheet for a quick-and-dirty check of goodness of fit to a distribution is not a bad idea, especially if somebody has handed you a batch of data in a spreadsheet or you are doing other spreadsheet analyses with these data (or if you want to check up on other software to confirm its accuracy or your understanding of its calculations). Here is what a chi-squared test might look like in a spreadsheet:
The chi-square statistic in this example is $10.37$ with a p-value of $0.409$. The data are singled out with a separate (blue) color; important values are highlighted; and auxiliary values (whose columns I usually hide) are shown in light gray text. (A few calculations are done as cross-checks, such as the values in the "Total/max" line (row D14:H14).)
To accomplish the test,
Before inspecting the data, set up a list of cutpoints (column D) that will define the "bins" into which the data will fall. For instance, if you expect the data to lie between $0$ and $10$ and you have $1500$ values, you might choose to divide this range into bins of widths somewhere between $0.2$ and $1$. (The smaller width of $0.2$ would give an average of $30$ data per bin, but likely some extreme bins would have much smaller counts; the larger width of $1$ gives only $10$ bins, which might only coarsely distinguish the distribution of data.) You do not have to put equal gaps between the bins. Often, for instance, the most extreme bins are made wider to accommodate expected sparse data in the tails of the distribution.
Compute the data counts in each bin (column F). In Excel, use COUNTIF to count data below or equal to each cutpoint (column E) and subtract each pair of successive counts to obtain counts in each bin.
Estimate the parameters of the distribution you are fitting, using Maximum Likelihood (cells B3:C4). (There's some fudging going on here; for more about this, see https://stats.stackexchange.com/a/17148.) For a Normal distribution, the Maximum Likelihood estimates are the mean (AVERAGE) and the uncorrected ("population") standard deviation (STDEVP).
Use the cumulative distribution function to obtain expected values in each bin. In Excel the CDF is NORMINV. In any platform, the arguments to the CDF are the distribution parameters and the upper bin endpoint. This gives expected total counts for all values up to and including the endpoint (column G). Therefore, subtract the values of the CDF at successive endpoints to obtain expected values in bins (column H). Notice how the calculation of the CDF parallels the use of COUNTIF to find bin counts: the bin counts are the empirical distribution while the CDF gives the reference distribution to which the empirical distribution will be compared.
Apply the chi-squared formula: subtract expected values from bin counts (the residuals); square them; divide by the expectations; add everything up (cell C6). (It is convenient, actually, to modify this a bit in practice: divide the residuals by the square roots of the bin counts (column I): these are interesting in their own right, because very positive or very negative ones indicate precisely how the data deviate from the reference distribution. The chi-squared statistic is the sum of squares of the residuals.)
Compute the chi-squared p-value (using CHIDIST) (cell C7).
Inspect the counts and the residuals. If a sizable proportion of counts are nonzero but less than $5$, the p-value is untrustworthy. If the residuals show a clear pattern, such as progressing steadily from negative to positive back to negative, then you might have evidence of lack of fit, regardless of the chi-squared result. (Plotting the residuals is a good idea, but is not shown here.)
Here are the formulas used in the example:
In this case all residuals are small in size; there is no pattern to them; and the chi-squared p-value is large. We conclude these data look Normally distributed. (In fact, they were generated using draws from a Normal distribution with mean $5$ and standard deviation $2$ via the formula NORMSINV(RAND())*2 + 5.)
Notice that the formulas make extensive use of named ranges. The names correspond systematically to the labels shown in the spreadsheet; for instance, Data is the range A:A headed by "Data" (column A). I warmly recommend always using this technique, because it creates readable formulas and readable formulas are formulas that tend to be correct.
Be careful when reproducing these formulas: although most of the formulas in columns E:I have just been copied down, often the very first and very last formulas in each column are a little different.
