1

I have a database with more than 50000 observations.

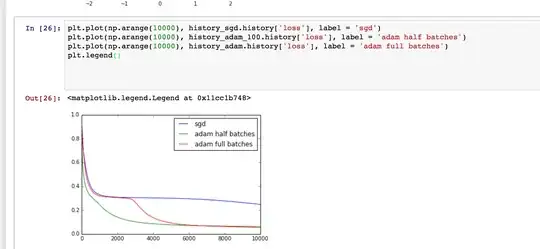
Histogram

For the determination of normality by means of statistical contrasts, since the Shapiro-Wilk test cannot be used due to the large number of observations, would it be better to use the Kolmogorov-Smirnov test or the Anderson-Darling test?

David E.S.
  • 97
  • 6
  • 1
    So, the first question has to be "what do you need this data to do for you?" Data does not become normal as it becomes large. What I am guessing that you are referring to is that if you were to repeatedly sample, the distribution of the sample averages would be normal. No amount of increase in the amount of data will make the data, itself, normal. – Dave Harris Apr 25 '21 at 21:56
  • Exactly, so... would be more rigorous if, in a table, I determine median and median absolute deviation instead of mean and standard deviation? Or, which option will be the best for describing non-normal variables statistically? Thank you for your answer :-) (you can post as an answer so that I can accept it!). – David E.S. Apr 25 '21 at 22:07
  • You’ve made a common mistake that is addressed in a question of mine from last year: https://stats.stackexchange.com/q/473455/247274. – Dave Apr 26 '21 at 02:53
  • @ DavidES. I have shown how you might use Shapiro-Wilk. If you are interested in a chi-squared goodness of fit of my fictitious data to normal, please say so, and I'll try to add that to my Answer tomorrow. – BruceET Apr 26 '21 at 09:32

1 Answers1

0

First, you hardly need a formal test with $n = 50\,000$ observations and such an obviously bimodal histogram.

There are various kinds of tests of normality.

  • The Shapiro-Wilk test, as implemented in R by shapiro.test, will take up to 5000 observations.
  • The Kolmogorov-Smirnov test, as implemented in R by ks.test, will test whether a sample follows a particular normal distribution. It would need to be modified, if $\mu$ and $\sigma$ were estimated from data.
  • A chi-squared test based on $k$ histogram bins, with $\mu$ and $\sigma$ estimated from the binned data, would have $k - 3$ degrees of freedom. Results might vary according how the data are binned to make the histogram.

Each of these tests would require some modification or pre-processing before use.

Because I don't have access to the data in your histogram, I will use somewhat similar fictitious data to illustrate a couple of possibilities.

set.seed(2021)
b = rbinom(50000, 1, .6)
x = rnorm(50000, 20.7, 1)
y = rnorm(50000, 24.2, 1.1)
z = b*x + (1-b)*y
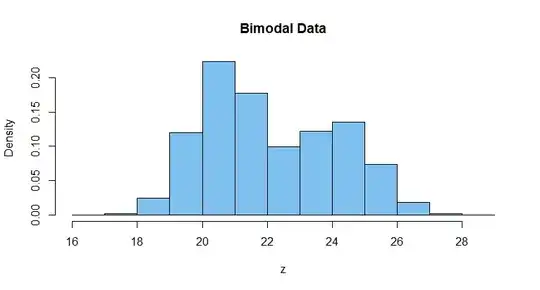
hist(z, prob=T, col="skyblue2", main="Bimodal Data")

enter image description here

One could sample $5000$ observations from among the $50\,000$ in z to use shapiro.test, to get an unequivocal rejection of the null hypothesis that data are normal, with a P-value very near $0.$

shapiro.test(sample(z, 5000))

    Shapiro-Wilk normality test

data:  sample(z, 5000)
W = 0.96129, p-value < 2.2e-16

I am not sure why shapiro.test is limited to 5000 observations. Perhaps it has to do with memory allocation or running time. However, it may make sense to limit a goodness-of-fit test in this way to avoid rejection on account of inconsequential quirks of the data that may have nothing to do with the purpose of testing for normality.

BruceET
  • 47,896
  • 2
  • 28
  • 76
  • Thanks for your answer! The problem is that my data contains ties and, as mentioned before, the number of observations is higher than the threshold admitted by the Shapiro-Wilk test. So I have tried to use the Anderson-Darling test to prove my data isn't normal. In this sense, I used directly the following sentence. `ad.test(DataBase$Variable)`. I don't know if the information is the same as the Shapiro-Wilk test, because I'm not familiarized with the AD test or the KS test. Which one would you use? – David E.S. Apr 26 '21 at 10:10
  • WIthout having a goal in mind it is hard to choose summary measures. And don't rely on statistical tests (which have power < 1.0) to guide you. Compute the empirical cumulative distribution function instead, possibly with confidence limits. – Frank Harrell Apr 26 '21 at 11:27
  • A-D is a worthy competitor of S-W to test goodness-of-fit to _some_ normal distribution. A-D is in an R library, not in the base of R. // The basic K-S is for testing GOF to a _particular_ normal dist'n with known $\mu$ and $\sigma.$ (But there are versions to take account of estimated parameters.) – BruceET May 28 '21 at 21:47