1

I am trying to understand the concept of ARCH(1) model from this tutorial video.
From 4:15, it's explained that,
the variance of residuals (1) can be formulated as (2).
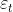(equation = residual at t, 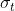equation=variance of residual(volatility) at t, w=white noise)

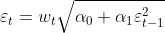equation (1)

equation (2)

However, as wiki says,

ARCH model ... describes the variance of the current error term or innovation as a function of the actual sizes of the previous time periods' error terms

and the variance of residuals can be written as (3).

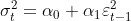equation (3)

I am very confused because what wiki says seems to contradict with what's explained in the said video.
(1) seems to correspond with the fact that ARCH model takes into account the previous volatility(variance of residuals).
(3) seems to correspond with the fact that ARCH model takes into account the previous time period's error terms (residuals).

Could anyone clarify how the (1) is re-formulated to (2) mathematically?
Also please tell me if there's anything that I seem to misunderstand.

Really appreciate your help.

koyamashinji
  • 269
  • 7

1 Answers1

0

The statement in the first video appears to be wrong. In particular, (1) is wrong while (2) is correct. (3) is also correct, and it agrees with (2). The second video regarding (1) is not wrong, but the relationship is more subtle than indicated by (1).

To see what happens if one tries to use (1) instead of (2), look at the graph in my answer in the tread "Does GARCH($p$,0) make sense at all?".

Generally, if you are unsure about a video, it may be a good idea to cross check with a respectable textbook. That could be Hamilton "Time Series Analysis", Tsay "Analysis of Financial Time Series", Zivot "Modeling Financial Time Series with S-PLUS" or some other one.

Richard Hardy
  • 54,375
  • 10
  • 95
  • 219
  • Thank you so much for clearing up my confusion! Could you elaborate a bit more on what you said "the relationship is more subtle than indicated by **(1)**"? Because to me, **(2)** does not seem to take into account the volatility, but the previous time period's error. – koyamashinji Apr 25 '21 at 13:33
  • @koyamashinji, previous time period's error comes from a distribution that has some variance, and that variance is $\sigma_{t-1}^2$. So $\sigma_{t-1}^2$ is there but only indirectly, i.e. through the realization $\varepsilon_{t-1}$. In other words, $\varepsilon_{t-1}$ comes from a distribution the variance of which is $\sigma_{t-1}^2$. – Richard Hardy Apr 25 '21 at 14:18